Запропонував своїм учням і вчителям інформатики у фейсбуці цікаву, як на мене, задачу:

Це вся умова, нічого більше в умові немає. Щоб не допускати вгадування, всі розв’язки просив пояснювати. Варіант «Я – художник, я так бачу» як варіант не приймався, бо задача була заявлена як логічна і потребує, відповідно, логічного пояснення.
Можете спробувати самостійно розв'язати, а лише після того клікнути на "Детальніше" і дізнатися ще кілька версій розв'язку.
Пропоную варіанти розв’язку, які я отримав. Але для початку давайте визначимося з елементами задачі. У нас є вісім фігур, із запропонованих «А» «Б» «В» «Г» нам треба згідно логічних міркувань обрати один варіант. Для зручності пронумеруємо фігури і визначимо, що як будемо називати.

Кожна фігура має контур – або тонкий або товстий або і тонкий і товстий одночасно. І кожна фігура має зірочку. В середині цієї зірочки може бути або пустота, як в фігурі номер сім, або коло, як у фігури номер два, або крапку, як у третьої фігури або одночасно і коло і крапку, як у фігури номер один. Ну і загальну фігуру, що складається з дев’яти фігур будемо називати матрицею.
Після того, як визначилися з тим, що як будемо називати, пропоную розглянути кілька логічних версій.
Версія 1. Де сьома фігура – головна. Запропонована Миколою.
Проведемо лінії від сьомої фігури:
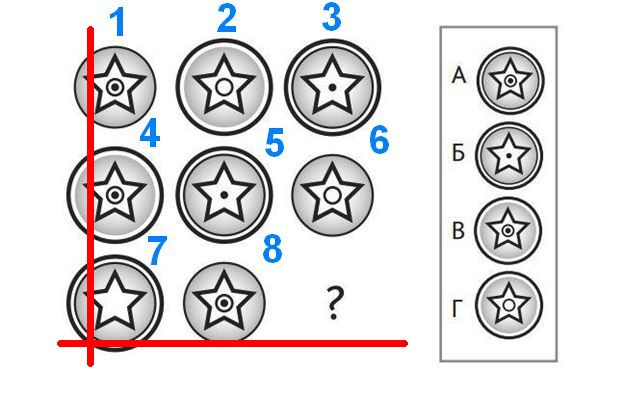
У вертикальному ряду, що складається з фігур 1, 4, 7 бачимо, що у нас є фігура з тонким контуром, товстим контуром і двома контурами одночасно. Крім того, у зірок всіх фігур, крім головної (сьомої) є одночасно всередині і крапка і коло. Такою самою логікою треба знайти фігуру з товстим контуром і зіркою з одночасно крапкою і колом. Очевидно правильна відповідь «В». На уточнююче запитання «а нащо тоді всі інші фігури?» учень відповів, що в умові задачі прямо не сказано, що треба аналізувати всі фігури. Не можу з ним не погодитися. Замовчування – то така тонка штука, може бути у кожного своє. Якщо в умові прямо не вказано використати всі елементи в логічних ланцюгах, то не можу цього вимагати.
Версія 2. Діагональна. Запропонована Валерієм і Олександром.

Якщо провести діагональ матриці через фігури 3, 5, 7, то всі фігури діагоналі мають товстий і тонкий контур. Вище і нижче діагоналі ми бачимо певну симетричність по контурам. Наприклад, фігури 2 і 4 мають однаковий товстий контур, а фігура 1 – тонкий. По такій самій логіці дев’ята фігура повинна мати товстий контур. Поки що це або «В» або «Г». Наповнення зірок всередині також певною мірою симетричне. 4=8, 2=6. Тому 1=9. І правильна відповідь по такій версії – «В».
Версія 3. Кутова. Запропонована Дариною.

Логіка для контурів: в кожному ряду і кожному стовбці є фігура з товстим контуром, з тонким контуром, з обома контурами. Тому дев’ята фігура повинна мати товстий контур, це варіант або «В» або «Г».
Для фігур всередині зірочок логіка така: Всі комбінації повинні бути унікальними. Пуста зірка є (фігура сім), зірка з крапкою є (фігура 3), зірка з колом є (це буде варіант «Г») і зірка з колом і крапкою також є (фігура 1). Правильна відповідь «Г».
Версія 4. Дві діагоналі і пропадаюча крапка. Запропонована Артемом.

Логіка для контурів така, як і в попередньому варіанті: в кожному ряду і кожному стовбці є фігура з товстим контуром, з тонким контуром, з обома контурами. Тому дев’ята фігура повинна мати товстий контур, це варіант або «В» або «Г».
Для фігур всередині зірочок логіка така: Розглядаємо діагональ з фігур 3-5-7. Крапка в третій фігурі і крапка в п’ятій. Якщо дві крапки, то вони знищують одна одну і в сьомій фігурі вже крапки немає.
Аналогічно, якщо розглядати діагональ 1-5-9 і ту саму логіку зникаючої крапки, то правильна відповідь «Г».
Версія 5. Пара елементів. Запропонована кількома авторами.
В кожному ряду і кожному стовбці кожен елемент повторюється двічі. Елементами (нагадаємо) ми називаємо: товстий контур, тонкий контур, коло в зірці, крапку в зірці. Правильна відповідь для такої версії – «В».
Версія 6. XOR. Запропонована кількома авторами.
Фукція XOR має таку бінарну карту:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0
Українською мовою логіку можна і по горизонталям і по вертикалях сформулювати так:
- Якщо в двох сусідніх фігурах нема однакових елементів – в третій фігурі ряду такий елемент також не з’явиться.
- Якщо елемент зустрічається лише в одній з сусідніх фігур, він буде і в третій фігурі ряду.
- Якщо елемент зустрічається в двох сусідніх фігурах, то він НЕ БУДЕ в третій фігурі ряду.
Особисто мені більше за все подобається остання версія, при цьому всі інші, як на мене, логічні.

