Відома задача, про яку чимало написано, як в серйозних виданнях по теорії ймовірностей так і на Вікіпедії.
Давайте спростимо умову до загальноголюдського розуміння. Якщо в певній групі людей, наприклад в шкільному класі буде 500 учнів, то яка вірогідність того, що два учні будуть мати однаковий день народження, тобто однакове число і один місяць? Звичайно, 100%. Ми зараз не говоримо про те, як буде виглядати нещасний класний керівник такого великого класу :) , ми про математику. А якщо в класі буде 366 дітей, а рік приймемо за 365 днів, то яка вірогідність? Так, знову 100%. У варіанті, коли дні народження перших 365 дітей розподіляться рівномірно на весь рік: 1 січня, 2 січня і т.д., то 366 по списку дитині вільних днів вже не залишиться, а це означає що його день народження співпаде з днем народження іншої дитини в класі. А тепер припущення:
У групі, що складається з 23 або більше осіб, ймовірність збігу днів народження (число і місяць) хоча б у двох людей перевищує 50%. Наприклад, якщо в класі 23 учня або більше, то більш імовірно те, що у когось з однокласників дні народження припадуть на один день, ніж те, що у кожного буде свій неповторний день народження.
На перший погляд – це неправда. Так, у моєї доньки в класі з 30 учнів є дві дівчини, що народилися в один день і місяць. В школі, де я працюю, так само співпадають дні народження двох вчителів інформатики. Але при порівняно невеликій групі з 23 осіб мати вірогідність більше ніж 50% - це, здається, математичною помилкою. Але – ні. В російськомовній Вікі дуже детально все розписано, саме її і раджу для системного аналізу.
А тепер задача з e-olymp.com на цю тему:
Дні народження
https://www.e-olymp.com/uk/problems/1317
Відомо, що у групі з 23 або більше людей ймовірність того, що хоча б у двох з них дні народження (число та місяць) співпадуть, перевищує 50%. Цей факт може здатись як таким, що протирічить здоровому глузду, так як ймовірність одному народитись у певний день року досить мала, а ймовірність того, що двоє народились у конкретний день – ще менша, але є вірним у відповідності з теорією ймовірності. Таким чином, факт не є парадоксом у строгому науковому сенсі – логічного протиріччя у ньому нема, а парадокс полягає лише у відмінностях між інтуїтивним сприйняттям ситуації людиною та результатами математичного розрахунку.
Для заданої кількості людей обчислити ймовірність того, що двоє з них народились у один день року. Рік вважати рівним 365 дням.
Вхідні дані
Кожен рядок є окремим тестом і містить кількість людей n (1 < n < 400).
Вихідні дані
Для кожного значення n в окремому рядку вивести ймовірність того, що хоча б у двох з n людей дні народження (число та місяць) співпадають. Шукану ймовірність виводити у відсотках і округлювати до 8 знаків після коми як показано у прикладі.
Ліміт часу: 1 секунда
Ліміт використання пам'яті: 64 MB
|
Вхідні дані |
Вихідні дані |
|
2 |
0.27397260% |
|
10 |
11.69481777% |
|
23 |
50.72972343% |
|
366 |
100.00000000% |
Джерело: Медведев М.Г. – «Зимняя школа в Харькове 2009»
Класифікація задачі: теорія ймовірностей
Давайте аналізувати. Вікі права:
У групі з 23 людей ймовірність збігу днів народження у двох людей настільки висока, тому що розглядається ймовірність збігу днів народження у будь-яких двох людей в групі. Ця ймовірність визначається кількістю пар людей, які можна скласти з 23 чоловік. Так як порядок людей в парах не має значення, загальне число таких пар дорівнює числу сполучень з 23 по 2, тобто (23 × 22) / 2 = 253 пари.
У формулюванні парадоксу мова йде саме про збіг днів народження у будь-яких двох членів групи. Одна з поширених помилок полягає в тому, що цей випадок плутають з іншим випадком, на перший погляд схожим, коли з групи вибирається одна людина, і оцінюється ймовірність того, що день народження будь-яких інших членів групи співпаде з днем народження цієї обраної людини. В такому випадку ймовірність збігу значно нижче.
Сподіваюсь, теорію на вікі вже прочитали. З математичної точки зору при рівномірному розподілі:

Наведене в червоному прямокутнику можна розписати математично:
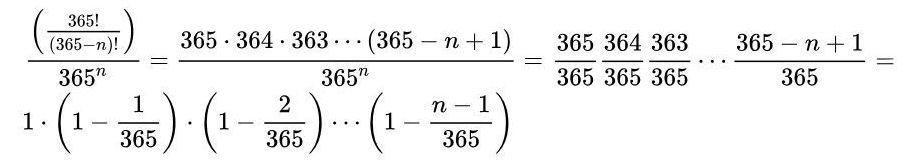
Ну а на Python наведене в червоному прямокутнику реалізується просто і елегантно:
x = 1
for i in range(2, n+1):
x *= 1 - (i-1)/365
Все інше – деталі. Робота з файлами описана, хто забув, у Пісочниці, в задачі «Робота з текстовими файлами в Python».
А для тих, хто забув про форматування виводу змінних в Python, існує довідник «input_print».
А в вашому класі скільки учнів? А в вашому класі є співпадіння днів народження?
Ps. Для учасників гуртка i7 здача задачі є обов’язковою, код мені в телеграм, будь ласка, PEP8, ага :)

