Розв’язок задачі про десять бочок меду
На даний час для розв'язку задачі запропоновано три підходи:
1) повний перебір
2) підбір з елементами аналізу
3) аналіз з підбором.
Повний перебір (мій):
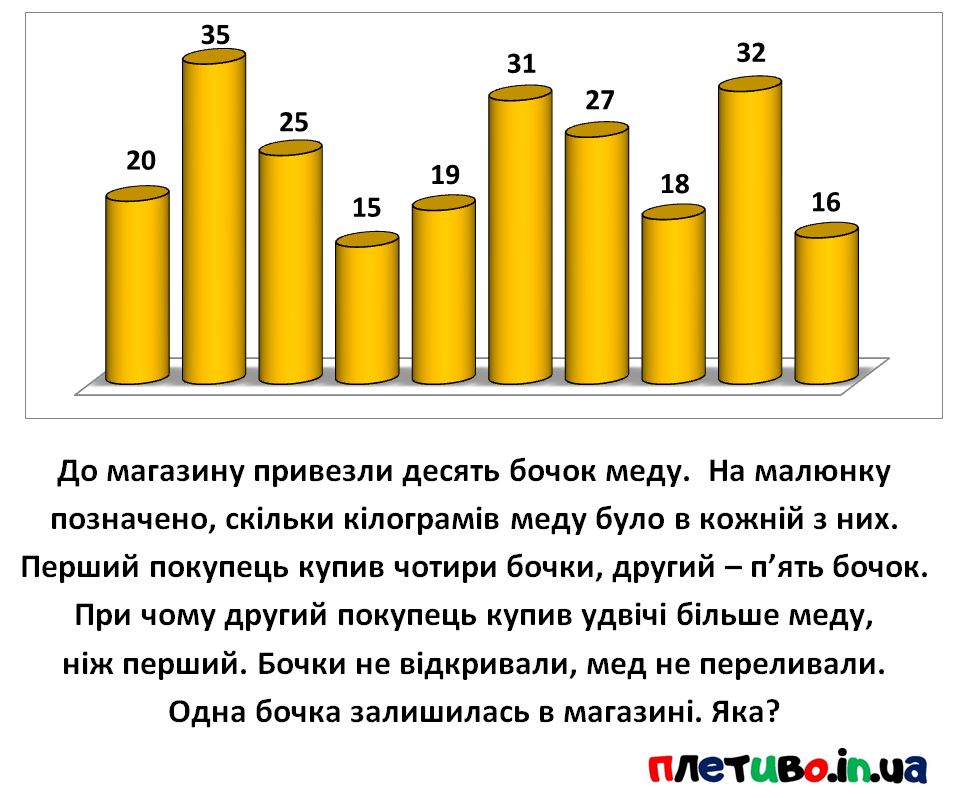
Давайте припустим, що в магазині залишилась перша бочка, в якій 20 кілограмів меду.
Тоді весь мед, що купили два покупця знаходиться в дев’яти бочках, в кілограмах це:
35 25 15 19 31 27 18 32 16
Припускаємо, що перші чотири бочки купив перший покупець. Тоді у нього буде
35 + 25 + 15 + 19 = 94 кілограми.
У другого покупця, відповідно:
31 + 27 + 18 + 32 + 16 = 124 кілограми.
Це, звичайно, не вдвічі більше ніж 94. Варіант не підходить.
Хтось запропонує відсортувати числа за зростанням і спробувати поділити на дві групи, може вийде. Пробуйте, не вийде. :)
Але якщо ми визначимо всі варіанти перестановок цих дев’яти чисел, то поділив числа на дві групи, ми знайдемо рішення. Проблема в тому, що число перестановок дев’яти чисел – це 9 факторіал. Хто не в курсі, це 1*2*3*4*5*6*7*8*9 = 362880. Тобто, перебравши таку кількість перестановок ми знайдемо розв’язок. Фактично ми знайдемо відповідь не на останній перестановці, але все одно знайдемо. При умові, звичайно, що лишнє число – 20.
До речі, в умові не сказано, скільки розв’язків має задача. Можливо, правильних розв’язків – декілька. Це значно ускладнює наш розв’язок методом перебору, бо нам треба перебрати взагалі всі варінти. Скільки це буде? Припускаємо, що у магазині залишилась перша бочка – 362880 перестановок. Припускаємо, шо в магазині залишилась друга бочка – знову 362880 перестановок.
А 362880 * 10 = 3628800. Більше 3,5 мільйонів варіантів.
Тут ще запитання формування цих самих перестановок. Якщо мова йде про Пайтон, то в стандартній бібліотеці, в модулі itertools є корисна нам функція permutations. Передаємо функції список, а вона повертає нам всі варіанти перестановок. Саме використання permutations дозволяє написати короткий елегантний код.
Коли програма знайде бочку, яка залишилась, програма повинна продовжувати шукати інші. Для того, щоб визначити кількість можливих розв’язків.
Я вклався в 9 рядків коду:
from itertools import permutations
start = [15,16,18,19,20,25,27,31,32,35]
for x in range(10):
minus_one = start.copy()
minus_one.remove(start[x])
kit = permutations(minus_one)
for i in kit:
if (i[0] + i[1] + i[2] + i[3]) * 2 == i[4] + i[5] + i[6] + i[7] + i[8]:
print(i[0],i[1],i[2],i[3],i[4],i[5],i[6],i[7],i[8], 'out', start[x])
Тут можна запустити мою програму на rep.it
https://repl.it/@ttolich/10barrelsofhoney
Другий варіант - підбір з елементами аналізу першим запропонував Валерій Шмідт.
Він підбирав і аналізував. Ось скріншот його роботи:
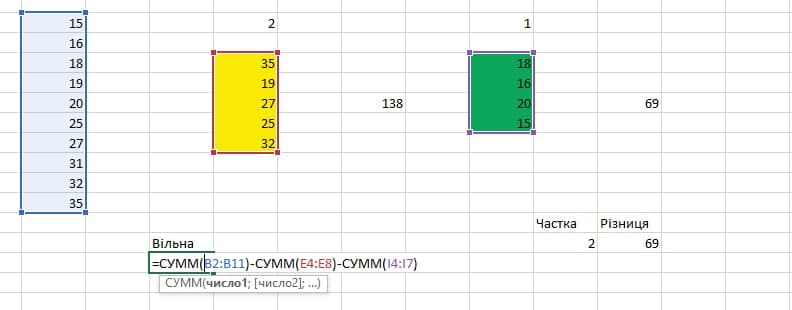
Пояснення Валерія: Переставляв вільну бочку, дивився на різницю і перевіряв частку.
Таким самим шляхом підбору і аналізу розв'язала задачу психолог Любов Возняк. Вона списала не одну сторінку блокноту в пошуках, зверніть увагу як гарно вона оформила відповідь:

Любов, я вже написав листа вашій шкільній вчительці математики. Вона зрадіє. Не дуже зрозуміло, чому вас, нелінивого логіка, понесло у психологію :)
Олексій Бірюченко, автор третьої концепції розв'язку, розпочав з аналізу:
Я прийняв 10 чисел за a1, a2, ..., a10, a суму за C. Причому a10 - число, яке ми шукаємо. Записав першу умову, з неї вивів рівняння, а з рівняння знайшов умову, яка дозволила з 10 можливих чисел a10 залишити 4.
Суть в тому, що ми шукаємо натуральні серед натуральних чисел, а це означає, що залишок від ділення повинен бути нульовим. Ну, а потім простим підбором мінімальних можливих a1, a2, a3, a4 знайшов потрібне А10. У мене вийшло, що залишиться бочка в 31л.

Ось такі у нас зібралися варіанти розв'язків задачі про десять бочок меду. Смачного дня! )

