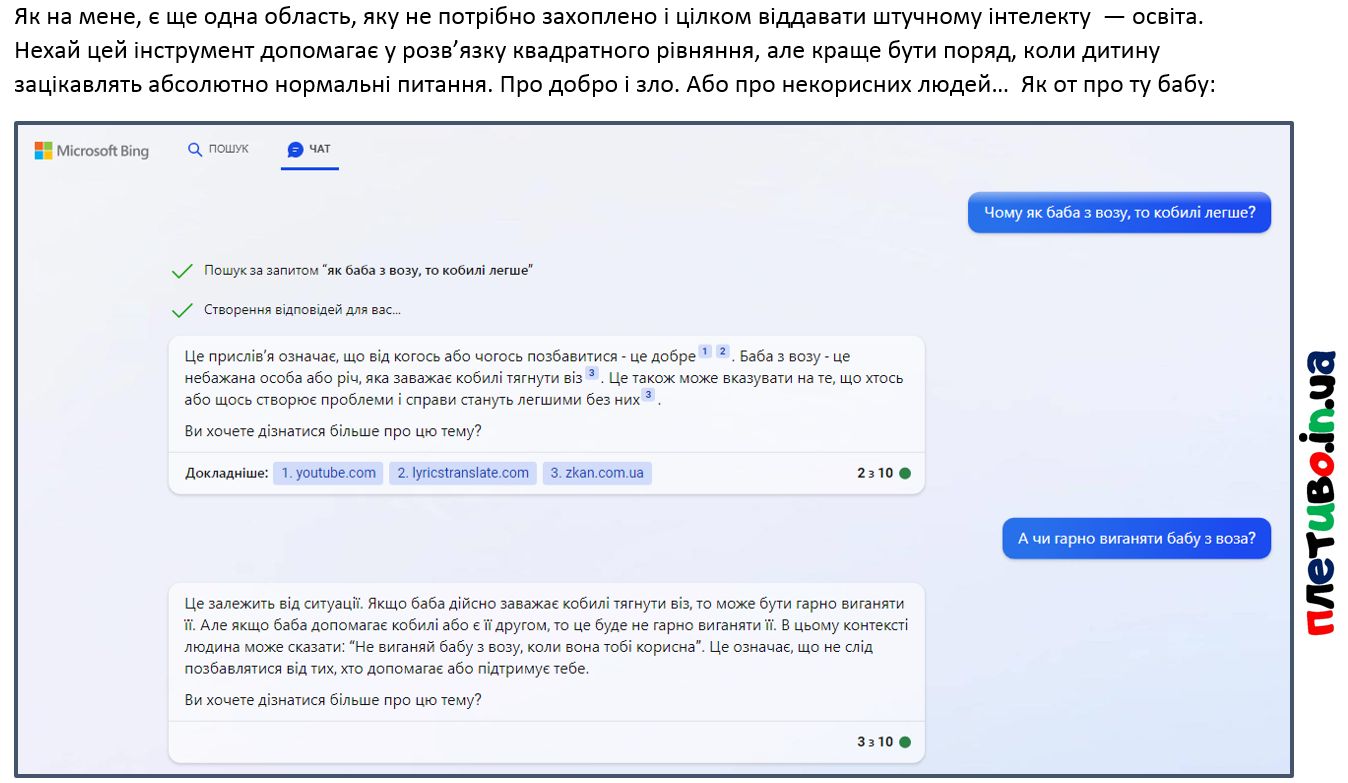
На гуртку i7, граємося математикою:
— Назвіть найбільший спільний дільник чисел 12 і 18?
— Шість.
— Добре, напишіть код що це визначить.
— print(math.gcd(12,18))
— Добре, назвіть найменше спільне кратне цих 12 і 18. Тобто НСК.
— Тридцять шість.
— Добре. Пишіть код, що це визначить.
— print(math.lcm(12,18))
— Ой, а ви де це взяли?
— ChatGPT підказав, у Python з версії 3.9
— Ну, тоді у нас сьогодні версія 3.8 і ChatGPT – гріх. Шукаємо НСК в нових умовах ))
Одного чудового ранку понеділка три друга – Вова, Петрик і Степан знайшли скарб з цукерками. Кожен в цей день з’їв купу цукерок, а дослідник Петрик записав всі кількості в зошит, бо йому було цікаво дізнатися загальну кількість цукерок у скарбі. У вівторок і середу щасливі дні продовжилися і хлопці радісно споживали смакоту. Але в четвер на перманентно-радісні обличчя хлопців звернула увагу Оленка. За допомогою різноманітних і не завжди коректних методів впливу вона дізналася про скарб і швидко сформувала у хлопців комплекс провини на предмет «треба було ділитися». Починаючи від четверга Оленка також взяла участь у смачних дегустаціях. В неділю цукерочний скарб вичерпався. Оленка заявила хлопцям, що вона в цій історії – постраждала сторона, бо почала брати участь у щасті лише з четверга, коли всі інші раділи вже на повну. Петрик дістав зошит, і порахував на Python кому скільки дісталося цукерок:
names = ['Вова', 'Петрик', 'Степан', 'Оленка']
vova = [15, 20, 22, 7, 12, 23, 16]
petryk = [13, 14, 12, 11, 13, 12, 9]
stepan = [12, 2, 13, 14, 15, 16, 17]
olenka = [29, 30, 31, 28]
sweets = [sum(vova), sum(petryk), sum(stepan), sum(olenka)]
print(names)
print(sweets)
Проста і гарна програма видала чесну статистику:
['Вова', 'Петрик', 'Степан', 'Оленка']
[115, 84, 89, 118]
Розумна Оленка переглянула код програми, результат, і, звичайно, все зрозуміла. Але вирішила пошуткувати і включила режим «я – дівчинка, я в цифрах не розуміюсь, мені намалювати краще». Петрик колись давно, ще коли не було ChatGPT читав, що для неймовірно популярної мови Python написано величезне море бібліотек. Відповідно, щось повинно бути і для візуалізації даних, це ж популярна задача. Петрик продовжив дослідження і здивовано дізнався, що для візуалізації на Python давно існує бібліотека Matplotlib, але ще більш цікавим для Петрика був факт, що не треба возитися з встановленням цієї бібліотеки в свій локальний Python, розбиратися з PIP та іншими деталями. Достатньо в коді свої програми на Replit вказати використання зовнішньої бібліотеки. І розумний Replit самостійно розбереться з її підключенням і всіма необхідними налаштуваннями. Відповідно, щоб для Оленки зробити картинку-діаграму треба дописати в програму Петрика всього ТРИ рядочка.
import matplotlib.pyplot as plt
names = ['Вова', 'Петрик', 'Степан', 'Оленка']
vova = [15, 20, 22, 7, 12, 23, 16]
petryk = [13, 14, 12, 11, 13, 12, 9]
stepan = [12, 2, 13, 14, 15, 16, 17]
olenka = [29, 30, 31, 28]
sweets = [sum(vova), sum(petryk), sum(stepan), sum(olenka)]
print(names)
print(sweets)
plt.pie(sweets, labels=names, autopct='%.0f%%')
plt.show()
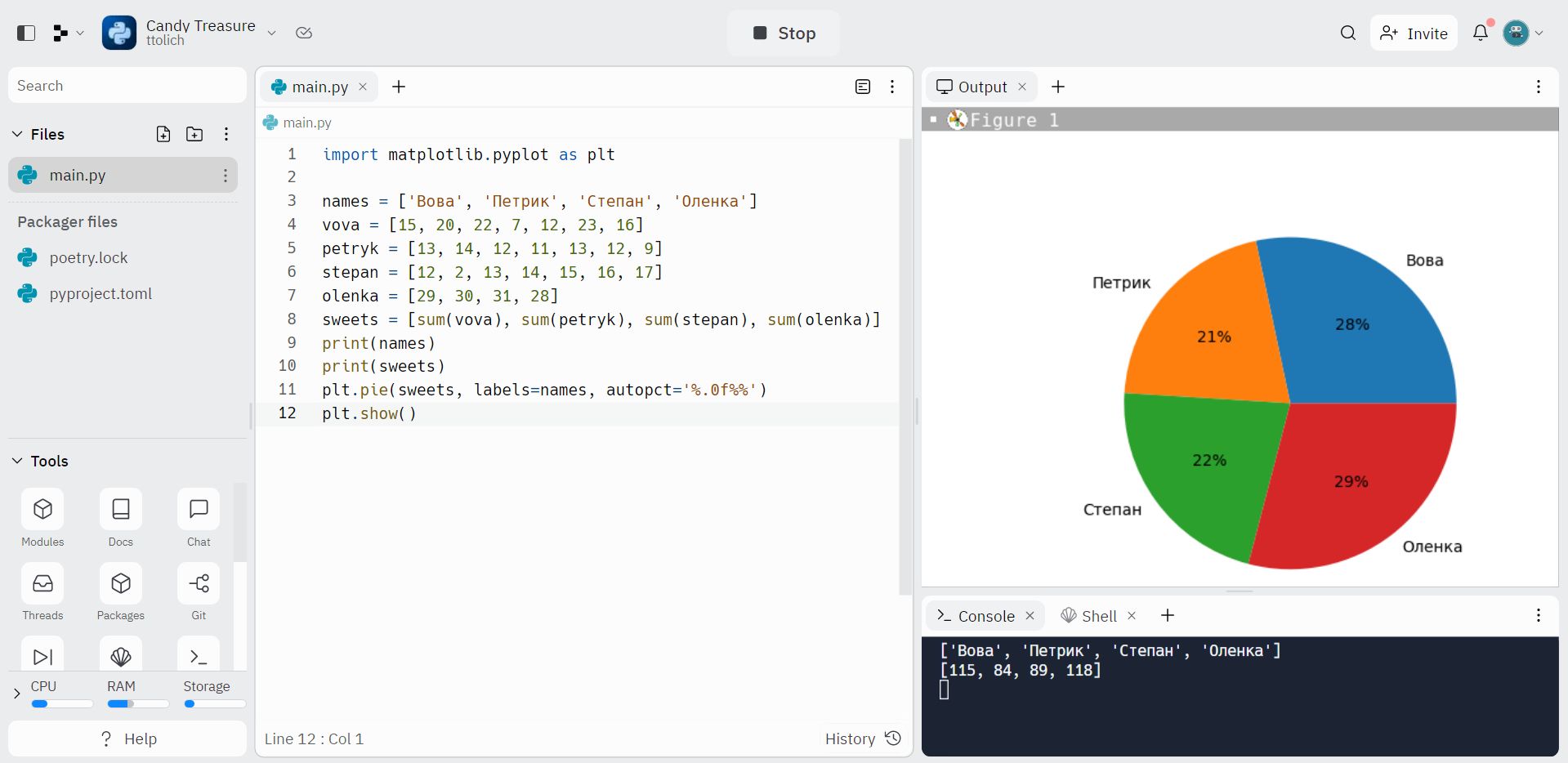
Яка краса! – сказала Оленка. Після чого вся компанія почала ще більше поважати Replit і знову-таки радіти Пайтону. Треба, — сказав Петрик, — знайти відповідну бібліотеку і порахувати вірогідність знаходження ще одного скарбу з цукерками. Це ж Python, обов’язково повинно на цю тему щось бути!
Звичайні шестигранні гральні кості бувають різні: праві і ліві, азіатські і європейські. Особливу увагу приділяють гральним костям для казино. На кожному екземплярі, зазвичай, проставляється логотип закладу та індивідуальний номер, для ускладнення шахрайства. На гранях костей для казино висвердлюють ямки, які заповнюються фарбою з такою самою щільністю, як вийнятий з ямок пластик, після чого кості полірують, щоб поверхня була ідеально гладкою. Такі кості називають «гладкокрапковими». Найчастіше, як пишуть, у казино зустрічаються кості з червоного прозорого пластику. Казино можуть продавати кості як сувеніри з недійсними серійними номерами:

Фото звідси
Всі ці складнощі щодо костей в казино мають просту мету – кості повинні видавати результати з максимальною рівномірністю. Давайте припустим, що в непрозорий кубик хтось всередину не по центру вплавить металеву кульку. Це скоріше за все змінить рівномірність результатів випадінь цифр і це шахрайство. Або хтось зробить кубик прозорим, але з нерівномірного пластику або некубічної, «витягнутої» або дещо «перекошеної» форми, – це, звичайно, також може змінити результати рівномірного випадіння цифр. Саме це і є, сподіваємось, причиною такого серйозного відношення до якості гральних костей у казино.
Ми можемо використовувати гральні кості для будь-яких своїх ігор. І хоч у нас тут не казино, ми хочемо мати нормальні гральні кості, без омани і хитрування, не витрачати купу грошей на щось, що називають «професійним».
Ось звичайні гральні кості, куплені в спортивному магазині:

Невеличкі, коштують по 2 гривні за штуку. Ставимо собі просту задачу – відібрати з них дві найкращі кості по рівномірності випадіння цифр. Наприклад, для використання в нашій грі. Звичайно, щодо ігор треба бути певною мірою обережними, бо, наприклад, грати в нарди канонічно заборонено в ісламі. Але зараз у нас тут не гра, а наукове дослідження, що буде складатися з суми експериментів і аналізу їх результатів.
Як інструмент для проведення аналізу нашого дослідження чудово підходить комп’ютер. Ми можемо скористатися електронною таблицею або написати програму мовою програмування. Звичайно, все можна порахувати за допомогою ручки і паперу, але використання комп’ютера виправдано – це зменшить об’єм ручної роботи і кількість помилок. А ще у нас є вже готовий математичний апарат дослідження – стандартне відхилення (standard deviation). Ще його називають середньоквадратичним відхиленням показників розсіювання значень випадкової величини відносно її математичного сподівання, тобто центру розподілу. Якщо це комусь здається дуже складним, то, запевняю, там дуже прості математичні обрахунки. Cтандартне відхилення просто рахується на листочку з ручкою і калькулятором, але на комп’ютері простіше і швидше. Чим менше величина стандартного відхилення, тим нам краще, тим рівномірніше випадають цифри. Якщо, наприклад, ми кинули гральну кість 12 разів і випало рівномірно: двічі одиниця, двічі двійка і т.д., то стандартне відхилення буде дорівнювати нулю.
Ось один з варіантів опрацювання результатів дослідження в електронній таблиці:
Перший експеримент, перше кидання кості. Випала, наприклад, одиниця. Ми записуємо в перший рядок (бо перший експеримент) одиничку в перший стовбчик (бо випала одиниця). При другому киданні цієї ж кості випала, припустим, трійка. Тоді записуємо одиничку в другий рядок (бо другий експеримент) в третій стовпчик (бо випала трійка). І так далі. В електронній таблиці потім дуже легко буде порахувати кількість випадіння кожної цифри, відсотки та однією формулою обрахувати стандартне відхилення.
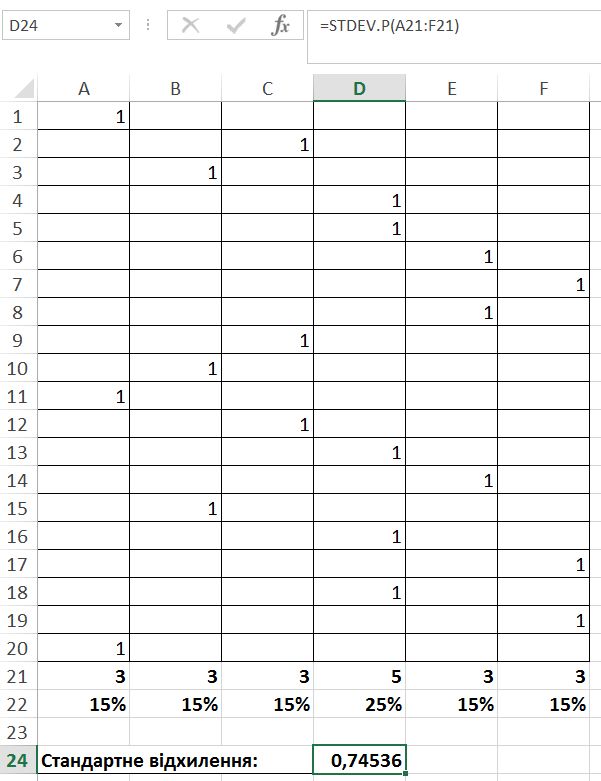
Звичайно, таку роботу можна проводити в парах – один учасник проводить експерименти, інший нотує їх результати. А ще можна порадіти існуванню електронних таблиць, бо рахувати стандартне відхилення на сотні експериментів вже достатньо довго.
Безумовно, задачу аналізу дослідження можна вирішити мовою програмування. І знову таки, чудовий завдяки своїй універсальності Python в стандартній бібліотеці має модуль statistics, в якому є функція обрахунку стандартного відхилення. Ось один з варіантів програми, що допоможе в аналізі:
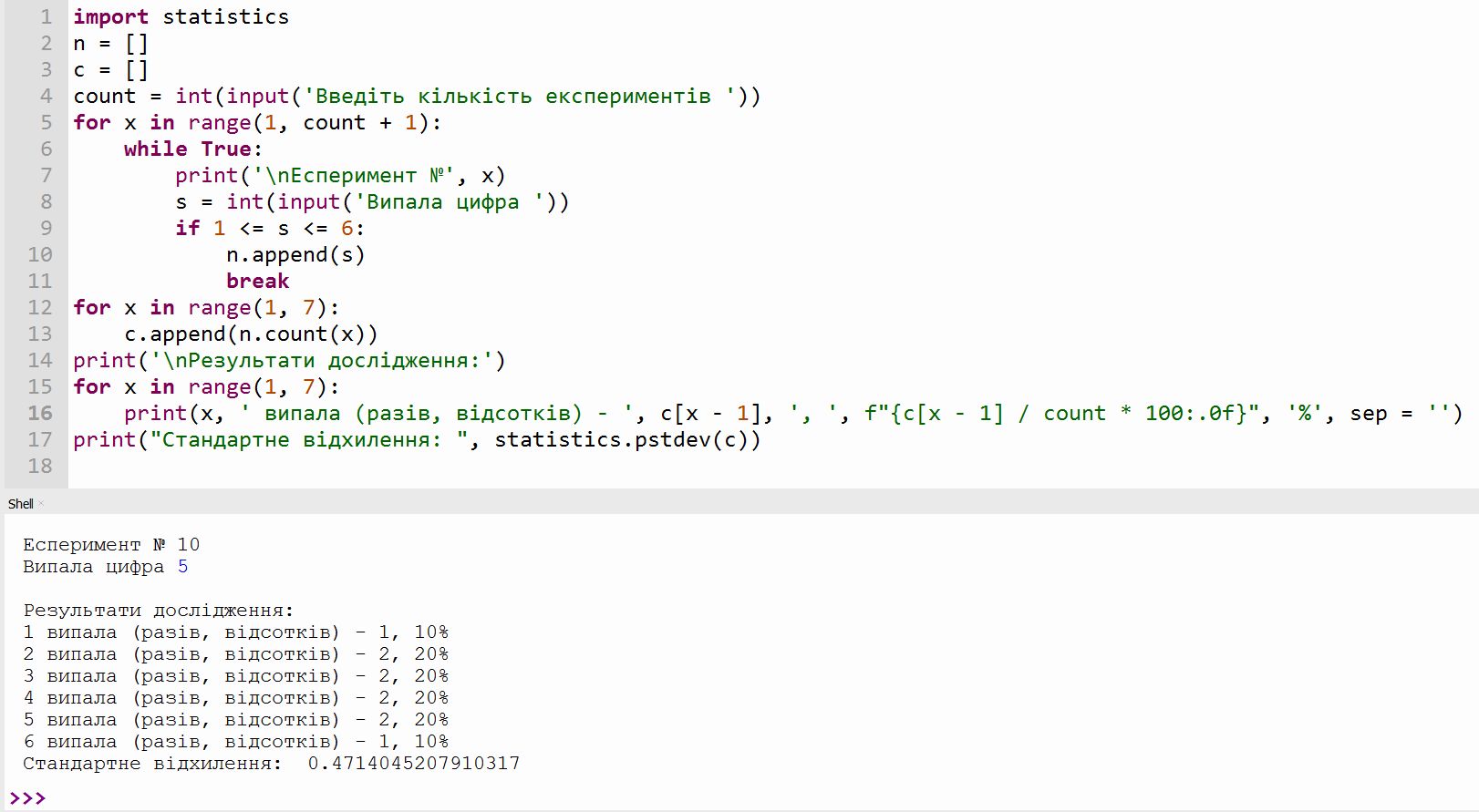
Код тут
Важливим в даному дослідженні є його прикладна сутність: ми за допомогою комп’ютера обирали дві гральні кості з найкращим показником рівномірності, причому обирали з науковим підходом і використанням чудового інструменту на ім’я комп’ютер. А ще розібралися з математичним апаратом такого дослідження. Це ж дослідження? Безумовно. З результатами? З результатами. Весела прикладна забава, частково відповідаюча на дитячі запитання «нашо та математика, для чого вона?!».