Сьогодні буде неолімпіадне програмування. Коли нема куди поспішати, є електрика в розетці і ароматний чай в улюбленій чашці. Сідайте поряд. Будемо розв’язувати задачу з сайту eolymp.com з номером 1536. Англійською ця задача зветься «Sweet Child Makes Trouble», а українською - «Улюблена дитина заважає», зловити б того креативного перекладача.
Умова:
Діти завжди любимі, але іноді вони можуть примусити вас вести себе різко. У цій задачі ви побачите, як Тінтін, п'ятирічний хлопчик, створює проблеми для своїх батьків. Тінтін - веселий хлопчик і завжди зайнятий справами. Але не все, що він робить, приносить радість його батькам. Більше всього йому подобається гратись з домашніми речами, як наприклад годинник батька або гребінець матері. Після гри він не повертає їх на місце. Тінтін дуже розумний хлопчик з достатнь чіткою памяттю. Він засмучує своїх батьків тим, що ніколи не повертає речі, взяті для гри, на їхнє місце.
Подумати лише! Якось вранці Тінтін вдалось викрасти три предмети домашнього вжитку. Скількома способами він може повернути ці речі так, щоб жоден з предметів не попав на своє попереднє місце? Тінтін не бажає засмучувати своїх батьків і приносити їм неприємноісті. Тому він нічого не ховає у нових місцях, а просто перекладає предмети.
Вхідні дані
Вхідні дані складаються з декількох тестів. Кожний тест містить натуральне число, яке не перевищує 800 - кількість речей, які Тінтін взяв для гри. Кожне число знаходиться у окремому рядку. Останній рядок містить -1 (мінус один) і не опрацьовується.
Вихідні дані
Для кожного тесту вивести кількість способів, якими Тінтін може повернути взяті речі.
Приклад вхідних даних:
2
3
4
-1
Приклад вихідних даних:
1
2
9
Давайте розбиратися.
Розглянемо варіант, коли Тінтін взяв дві речі. Якщо одну річ позначити одиничкою, а другу - двійкою, то варіант перестановки один:
12 (стартовий)
21 (перестановка)
Розглянемо варіант, коли Тінтін взяв три речі. Одну річ позначимо одиничкою, а другу – двійкою, третю – трійкою. Пам’ятаємо, що згідно умови Тінтін не може класти речі на ті місця, звідки брав. Тобто, якщо в стартовій позиції одиничка на першому місці, но в жодній перестановці одиничка на першому місці бути не може. Тому варіанти будуть такими:
123 (стартова)
231 (перестановка)
312 (перестановка)
Це, до речі, підтверджує тестовий приклад, при трьох речах перестановок з даними умовами існує дві.
Розглянемо варіант, коли Тінтін взяв чотири речі. Тут варіанти перестановок будуть такими:
1234 (стартова)
2143 (перестановка)
2341 (перестановка)
2413 (перестановка)
3142 (перестановка)
3412 (перестановка)
3421 (перестановка)
4123 (перестановка)
4312 (перестановка)
4321 (перестановка)
Таку кількість ще можна перебрати вручну. А от цікаво, а для п’яти речей скільки перестановок? Очікувано буде чимало, але то скільки в цифрах? Тут можна, потайки від математиків, знайти рішення перебором:
start = '12345'
c = 0
for x1 in range(1,6):
for x2 in range(1,6):
for x3 in range(1,6):
for x4 in range(1,6):
for x5 in range(1,6):
if x1 != 1 and x2 != 2 and x3 != 3 and x4 != 4 and x5 != 5 and len(set([x1,x2,x3,x4,x5])) == 5:
c += 1
print(x1, x2, x3, x4, x5, sep = '')
print(c)
У нас вийшло 44 перестановки:
21453
21534
23154
23451
23514
24153
24513
24531
25134
25413
25431
31254
31452
31524
34152
34251
34512
34521
35124
35214
35412
35421
41253
41523
41532
43152
43251
43512
43521
45123
45132
45213
45231
51234
51423
51432
53124
53214
53412
53421
54123
54132
54213
54231
Особисто я десь глибоко всередині відчуваю, що десь поряд ховається розумний математичний розв’язок. Десь дуже глибоко. У нас вже ж є послідовність, залежність кількості перестановок від кількості речей. Ось:
Кількість речей – кількість перестановок:
2 – 1
3 – 2
4 – 9
5 – 44
Так як у нас не олімпіада, а посиденьки з електрикою і чаєм, то давайте, поки математики знову не бачать, заглянемо до них в енциклопедію цілочислових послідовностей, у нас вже є чотири елементи послідовності: 1, 2, 9, 44
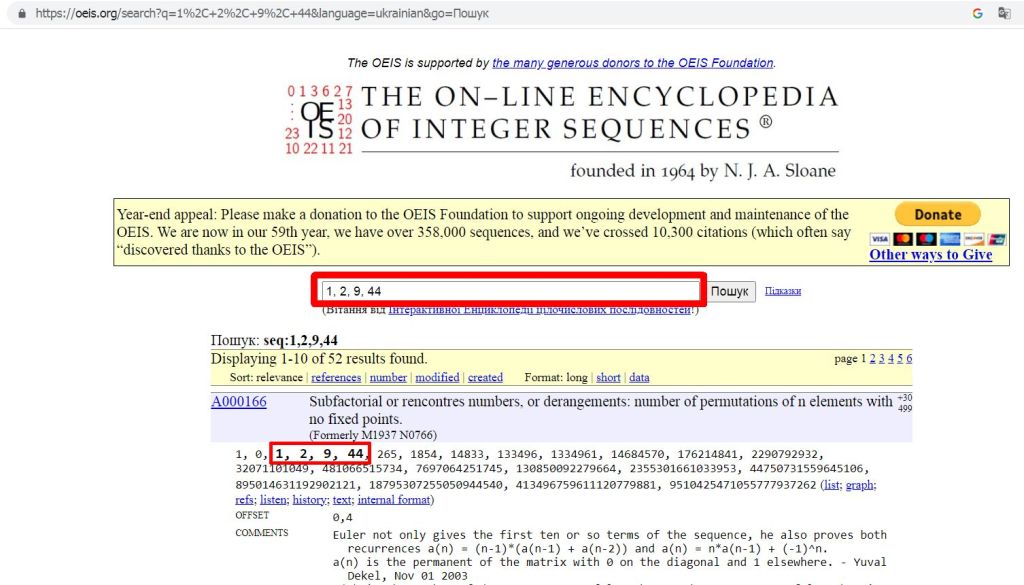
Отримуємо щось страшне і по суті і англійською ))
І в довгих і страшних поясненнях для розумних математиків відшукуємо нам потрібну формулу! ))

Ну а далі вже просто. Тепер можна кликати математиків і ховати перебор. І розв’язати задачу, коли наступний член послідовності визначається формулою:
a(n) = n*a(n-1) + (-1)^n
У вигляді Пайтон-програми це може бути, наприклад, так:
while True:
c = int(input())
if c == -1:
break
else:
a = 0
for n in range(2, c + 1):
a = n * a + (-1) ** n
print(a)
Яка у них, математиків, гарна наука, так? )

