Пропоную розглянути чудову задачу «Булочки» з сайту eolymp.com. Безумовним плюсом задачі, як на мене, є простота умови і чудова родзинка, яку психологи називають «розрив шаблону».
Булочки
https://www.eolymp.com/uk/problems/11379
Умова:
Хусейн дуже любить булочки, які продаються в університеті. Відомо, що
- можна купити одну булочку за a гяпиків;
- можна купити три булочки за b гяпиків;
Хусейн хоче придбати точно n булочок. Яку найменшу кількість гяпиків йому слід витратити?
Вхідні дані:
Три натуральні числа a, b і n, кожне з яких не більше 10^9.
Вихідні дані:
Виведіть найменшу кількість гяпиків, яку слід витратити Хусейну для покупки точно n булочок.
Приклад
Вхідні дані :
2 5 10
Вихідні дані:
17
Автор: Михаил Медведев
Розглянемо тестовий приклад. Одна булочка коштує два гяпіка. Але три булочки коштують не шість, а п’ять гапіків. Ми бачимо зрозумілу оптову ціну. Якщо купити відразу три, то кожна булочка буде трохи дешевше, а саме 5 / 3 = 1,67 гяпіка. Очевидно, що при оптових знижках нам варто купити якомога більше «трійок булочок», а вже далі доповнити нашу купівлю одиночними, більш дорогими булочками.
В тестовому прикладі нам треба купити 10 булочок. Давайте порахуємо максимальну кількість трійок, що ми можемо купити. 10 // 3 = 3. Тобто ми можемо купити три рази по три булочки і таким чином заплатимо 5 + 5 + 5 = 15 гяпіків. Це так ми купимо дев’ять булочок. Ну а десяту вже купимо подорожче, за два гяпіка.
В булочках у нас буде така купівля: три + три + три + одна.
В грошах у нас буде така купівля: 5 + 5 + 5 + 2 = 17.
Ці 17 гяпіків – це і є відповідь, яку ми бачимо в тестовому прикладі.
І якщо ми напишемо код, то здамо задачу… лише на 80%. А чого?
А тому що автор гарно підказав нам типовий приклад. І тому що ми всі звикли, що оптом – дешевше. Це – шаблон. Але… А хто нам обіцяв, що так завжди? А давайте знайдемо розв’язок, коли будуть такі умови:
2 (ціна однієї одиночної булочки)
7 (ціни трьої булочок, от такий дивний опт, а хто сказав, що не буває?)
10 (скільки Хусейну треба купити булочок)
Звичайно, що тоді Хусейну і дарма не треба такі оптові ціни, бо поштучно булочки дешевше.
Гарна задача, так?
То здавайте! )
Розв’яжемо задачу «Гарне число»
https://www.eolymp.com/uk/problems/7817
Умова:
«Гарним» будемо вважати число, що складається лише з непарних цифр. Наприклад число 157953 гарне, а число 2452117 ні. Необхідно з'ясувати, скільки існує n - значних гарних чисел.
Вхідні дані
Одне ціле невід'ємне число n (1 ≤ n ≤ 20).
Вихідні дані
Вивести кількість гарних чисел.
Приклад
Вхідні дані
4
Вихідні дані
625
Розпочнемо з аналітики.
Якщо числа одноцифрові, тобто n = 1, то таких чисел десять: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Серед них гарних буде п’ять: 1, 3, 5, 7, 9.
Якщо числа двоцифрові, тобто n = 2, то таких чисел всього дев’яносто, від 10 до 99. За допомогою листочка і ручки можна за незначний час порахувати кількість гарних чисел – їх буде 25.
При n = 3 можна також порахувати кількість гарних чисел за допомогою листочка, але то ліньки, бо тризначних чисел аж 900.
При n = 4 ми вже маємо відповідь з тестового прикладу задачі, тому можна спробувати зловити формулу залежності n і результату:
1 >> 5
2 >> 25
3 >> ?
4 >> 625
Якщо ви вже бачите тут формулу – чудово, здавайте задачу. Якщо не бачите, давайте спробуємо порахувати кількість гарних чисел для n = 3.
Уточнимо задачу.
Нам потрібно перебрати всі числа від 100 до 999 і в кожному числі визначити, чи складається число лише з непарних цифр. Звичайно, за допомогою циклу можна перебрати всі числа, за допомогою вкладеного циклу перебрати цифри кожного числа. Але якщо писати на Python, то повинно бути більш гарне і стильне рішення ніж перебір вкладеними циклами.
Пропоную скористатися множинами — структурами даних, що містять невпорядковані елементи, які не повторюються. Давайте кожне число з діапазону 100…999 переведемо в множину, таким чином позбавимося повторів цифр в числі. А далі порівняємо цю множину з множиною непарних чисел. Якщо множина конкретного числа менше або дорівнює множини непарних чисел, то це буде означати, що число складається лише з непарних чисел.
Для незнайомих з множинами, на «Плетиві» є відповідний довідник, побудований по принципу «менше тексту, більше прикладів».
За допомогою наступного коду з використанням множин ми зможемо визначити кількість гарних тризначних чисел:
count = 0
odd = {'1','3','5','7','9'}
for number in range(100,1000):
digits = set(str(number))
if digits <= odd:
count +=1
print(count)
Відповідно, зловити формулу тепер стає простіше:
1 >> 5
2 >> 25
3 >> 125
4 >> 625
Якщо так і не видно формули, то звертаємось до екциклопедії цілочислових послідовностей, де в перших рядках і бачимо шукану формулу:
https://oeis.org/A000351
Успіхів!
Сьогодні буде неолімпіадне програмування. Коли нема куди поспішати, є електрика в розетці і ароматний чай в улюбленій чашці. Сідайте поряд. Будемо розв’язувати задачу з сайту eolymp.com з номером 1536. Англійською ця задача зветься «Sweet Child Makes Trouble», а українською - «Улюблена дитина заважає», зловити б того креативного перекладача.
Умова:
Діти завжди любимі, але іноді вони можуть примусити вас вести себе різко. У цій задачі ви побачите, як Тінтін, п'ятирічний хлопчик, створює проблеми для своїх батьків. Тінтін - веселий хлопчик і завжди зайнятий справами. Але не все, що він робить, приносить радість його батькам. Більше всього йому подобається гратись з домашніми речами, як наприклад годинник батька або гребінець матері. Після гри він не повертає їх на місце. Тінтін дуже розумний хлопчик з достатнь чіткою памяттю. Він засмучує своїх батьків тим, що ніколи не повертає речі, взяті для гри, на їхнє місце.
Подумати лише! Якось вранці Тінтін вдалось викрасти три предмети домашнього вжитку. Скількома способами він може повернути ці речі так, щоб жоден з предметів не попав на своє попереднє місце? Тінтін не бажає засмучувати своїх батьків і приносити їм неприємноісті. Тому він нічого не ховає у нових місцях, а просто перекладає предмети.
Вхідні дані
Вхідні дані складаються з декількох тестів. Кожний тест містить натуральне число, яке не перевищує 800 - кількість речей, які Тінтін взяв для гри. Кожне число знаходиться у окремому рядку. Останній рядок містить -1 (мінус один) і не опрацьовується.
Вихідні дані
Для кожного тесту вивести кількість способів, якими Тінтін може повернути взяті речі.
Приклад вхідних даних:
2
3
4
-1
Приклад вихідних даних:
1
2
9
Давайте розбиратися.
Розглянемо варіант, коли Тінтін взяв дві речі. Якщо одну річ позначити одиничкою, а другу - двійкою, то варіант перестановки один:
12 (стартовий)
21 (перестановка)
Розглянемо варіант, коли Тінтін взяв три речі. Одну річ позначимо одиничкою, а другу – двійкою, третю – трійкою. Пам’ятаємо, що згідно умови Тінтін не може класти речі на ті місця, звідки брав. Тобто, якщо в стартовій позиції одиничка на першому місці, но в жодній перестановці одиничка на першому місці бути не може. Тому варіанти будуть такими:
123 (стартова)
231 (перестановка)
312 (перестановка)
Це, до речі, підтверджує тестовий приклад, при трьох речах перестановок з даними умовами існує дві.
Розглянемо варіант, коли Тінтін взяв чотири речі. Тут варіанти перестановок будуть такими:
1234 (стартова)
2143 (перестановка)
2341 (перестановка)
2413 (перестановка)
3142 (перестановка)
3412 (перестановка)
3421 (перестановка)
4123 (перестановка)
4312 (перестановка)
4321 (перестановка)
Таку кількість ще можна перебрати вручну. А от цікаво, а для п’яти речей скільки перестановок? Очікувано буде чимало, але то скільки в цифрах? Тут можна, потайки від математиків, знайти рішення перебором:
start = '12345'
c = 0
for x1 in range(1,6):
for x2 in range(1,6):
for x3 in range(1,6):
for x4 in range(1,6):
for x5 in range(1,6):
if x1 != 1 and x2 != 2 and x3 != 3 and x4 != 4 and x5 != 5 and len(set([x1,x2,x3,x4,x5])) == 5:
c += 1
print(x1, x2, x3, x4, x5, sep = '')
print(c)
У нас вийшло 44 перестановки:
21453
21534
23154
23451
23514
24153
24513
24531
25134
25413
25431
31254
31452
31524
34152
34251
34512
34521
35124
35214
35412
35421
41253
41523
41532
43152
43251
43512
43521
45123
45132
45213
45231
51234
51423
51432
53124
53214
53412
53421
54123
54132
54213
54231
Особисто я десь глибоко всередині відчуваю, що десь поряд ховається розумний математичний розв’язок. Десь дуже глибоко. У нас вже ж є послідовність, залежність кількості перестановок від кількості речей. Ось:
Кількість речей – кількість перестановок:
2 – 1
3 – 2
4 – 9
5 – 44
Так як у нас не олімпіада, а посиденьки з електрикою і чаєм, то давайте, поки математики знову не бачать, заглянемо до них в енциклопедію цілочислових послідовностей, у нас вже є чотири елементи послідовності: 1, 2, 9, 44
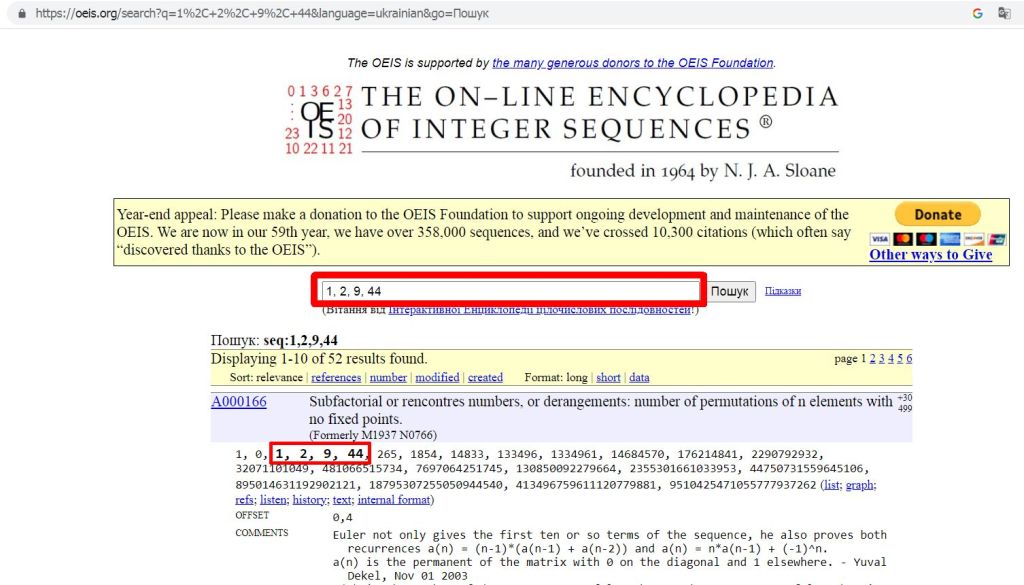
Отримуємо щось страшне і по суті і англійською ))
І в довгих і страшних поясненнях для розумних математиків відшукуємо нам потрібну формулу! ))

Ну а далі вже просто. Тепер можна кликати математиків і ховати перебор. І розв’язати задачу, коли наступний член послідовності визначається формулою:
a(n) = n*a(n-1) + (-1)^n
У вигляді Пайтон-програми це може бути, наприклад, так:
while True:
c = int(input())
if c == -1:
break
else:
a = 0
for n in range(2, c + 1):
a = n * a + (-1) ** n
print(a)
Яка у них, математиків, гарна наука, так? )
Джерело задачі: Збірник завдань для державної підсумкової атестації з інформатики. Автори: Н.В. Морзе, В.П. Вембер, О.Г. Кузьмінська, М.О. Войцеховський, Т.Г. Проценко. Рекомендовано Міністерством освіти і науки України. 2011 рік. 11 клас.
Варіант 7. Завдання 16: запишіть програму відомою вам мовою програмування. Вхідні дані вводяться з клавіатури, а вихідні дані виводяться на екран монітора.
Умова:
Дано натуральне число N (8 ≤ N ≤ 1000000), яке визначає будь-яку цілочислову грошову суму ≤ 1000000. Відомо, що цілочислову грошову суму, більшу чи рівну 7 грошовим одиницям, можна видати лише купюрами номіналом у 2 та 5 грошових одиниць. Визначте, якою кількістю купюр у 2 та 5 грошових одиниць можна видати суму в N грошових одиниць, щоб їхня загальна кількість була найменшою.
Кожен бажаючий може зімітувати собі ДПА в 11 класі, для цього достатньо зайти за посиланням на сайт eolymp.com і в швидкому режимі спробувати здати цю задачу однією з наступних мов програмування: С, С++, С#, D, Dart, Go, Haskel, Java, Javascript, Cotlin, Lua, MySQL, Pascal, Perl, PHP, Python, Ruby, Rust. Для роботи на сайті необхідно зареєструватися і підтвердити email. Все безкоштовно.
Давайте спробуємо розв’язати, нехай, за тридцять хвилин, добре? Відмітьте час початку, старт!
Посилання: https://www.eolymp.com/uk/problems/2033
Спробували? Тоді ще більше десяти варіантів розв'язку )
Ця задача відкриває книгу «Олімпіадна інформатика» В.Л.Дідковського і С.В.Матвійчука 2010 року. Умова:
Нумерація
https://www.e-olymp.com/uk/problems/109
Для нумерації m сторінок в книжці використано n цифр. По заданому n вивести m або 0, якщо розв’язку не існує. Нумерація починається з першої сторінки.
Вхідні дані
Єдине число n. У книзі не більше 7000 сторінок.
Вихідні дані
Вивести кількість сторінок у книзі.
Приклад вхідних даних:
27
Приклад вихідних даних:
18
Ліміт часу 1 секунда
Ліміт використання пам'яті 128 MiB
Автор: Сергій Матвійчук
Джерело: ІІ етап Всеукраїнської олімпіади в Житомирській області (2003)
Олімпіадне програмування відбувається у вкрай обмеженому проміжку часу. Але у нас зараз не олімпіада, тому пропоную підходити до задачі не поспішаючи, намагаючись підготувати її розв’язок як для співбесіди щодо прийняття на роботу.
Розберемо умову задачі. Перша сторінка нумерується цифрою один. Нам навіть не принципово якою саме, нам важливо, що ця цифра одна. Отже, для книжки з 1 сторінки використовується одна цифра, для книжки з двох сторінок використовується дві цифри, якщо конкретно це 1 і 2. Для книжки з 10 сторінок використовується 11 цифр, а саме: 1 2 3 4 5 6 7 8 9 1 0. У нашому тестовому прикладі, для книги з 18 сторінок використовується 27 цифр: 1 2 3 4 5 6 7 8 9 1 0 1 1 1 2 1 3 1 4 1 5 1 6 1 7 1 8. Нашою задачею є визначити кількість сторінок по числу цифр.
Може бути ситуація, коли по числу цифр визначити кількість сторінок неможливо. Наприклад, якщо кількість цифр у нумерації сторінок – 26.
Очевидно, якщо номер сторінки однорозрядний (від 1 до 9), то і кількість цифр, що потрібні для нумерації кожної такої сторінки – одна. При нумерації дворозрядних номерів сторінок (від 10 до 99), для нумерації кожної сторінки потрібні дві цифри і т. д. Кількість цифр, необхідних для нумерації сторінки змінюється, коли номер сторінки змінює розрядність, стає 10, 100, 1000. Тобто, 10x.
Задачу можна розв’язати за допомогою циклу. Будемо збільшувати номер сторінки і зберігати кількість цифр для нумерації поточної сторінки і загальну кількість цифр для нумерації всіх сторінок книги. Завершуємо цикл, коли кількість цифр для нумерування книги дорівнює або перевищує ту, що ми отримали на початку програми у вигляді вхідних даних. При рівності цих змінних необхідно вивести кількість сторінок, інакше — розв’язків не існує і виводимо нуль.
Далі розглянемо класичну цитату Роберта Мартіна з його класичної книги «Чистий код»:
Ім'я змінної, функції або класу має відповідати на всі головні питання. Воно повинно повідомити, чому ця змінна (і т. д.) існує, що вона робить і як використовується. Якщо ім'я вимагає додаткових коментарів, то воно не передає намірів програміста.
int d; // Минулий час
Ім'я d не передає абсолютно нічого. Воно не асоціюється ні з часовими інтервалами, ні з днями. Його слід замінити іншим ім'ям, яке буде вказувати, що саме вимірюється і в яких одиницях:
int elapsedTimeInDays;
int daysSinceCreation;
int daysSinceModification;
int fileAgeInDays;
Змістовні імена істотно спрощують розуміння і модифікацію коду (кінець цитати).
Якщо проходити співбесіду в місця з цікавими зарплатами, то існує висока вірогідність, що там книги Мартіна читали. Тим більше варто прислухатися.
Визначимо простір імен змінних у стилістиці Python:
input_sum_digits - (вхідна сума цифр) - кількість цифр, з яких складається книжка, вхідні дані
sum_digits (сума цифр) – змінна, в якій ми будемо накопичувати суму і порівнювати з input_sum_ digits для завершення роботи циклу
current_page_number (номер поточної сторінки) – в змінній зберігатиметься номер сторінки, що опрацьовується при поточній ітерації циклу
number_of_digits_on_current_page (кількість цифр на поточній сторінці) – очевидна величина.
Код з використанням змістовних імен достатньо зрозумілий:
input_sum_digits = int(input())
sum_digits = 0
current_page_number = 0
number_of_digits_on_current_page = 1
while sum_digits < input_sum_digits:
current_page_number += 1;
if current_page_number == (10 ** number_of_digits_on_current_page):
number_of_digits_on_current_page += 1
sum_digits += number_of_digits_on_current_page
if sum_digits == input_sum_digits:
print(current_page_number)
else:
print(0)
Ось усе це у стилістиці c#:
using System;
namespace MyApp
{
class Program
{
static void Main(string[] args)
{
int sumDigits = 0;
int currentPageNumber = 0;
int numberOfDigitsOnCurrentPage = 1;
int inputSumDigits = int.Parse(Console.ReadLine());
while (sumDigits < inputSumDigits)
{
currentPageNumber++;
if (currentPageNumber == Math.Pow(10, numberOfDigitsOnCurrentPage))
{
numberOfDigitsOnCurrentPage++;
}
sumDigits += numberOfDigitsOnCurrentPage;
}
if (sumDigits == inputSumDigits)
{
Console.WriteLine(currentPageNumber);
}
else
{
Console.WriteLine(0);
}
}
}
}
Погодьтесь, використання змістовних імен значно спрошує розуміння коду і для самого себе. Уявіть, що ви повернетеся до вашого коду розміром з сотню рядків через рік. Вам спростить розуміння коду використання змістовних імен? А тепер уявіть іншу ситуацію, коли вам треба на фоні дедлайну модифікувати сотні рядків чужого спагетті-коду, створеного з використанням неочевидних імен змінних, класів, методів. Як вам? Нікому не подобається, тож і ви так не пишіть )



