Сайт «Плетиво» запрошує всіх бажаючих анонімно пройти тест на знання круп.

Сайт «Плетиво» запрошує всіх бажаючих анонімно пройти тест на знання круп.


Давня історія, але може кому сподобається ідея для колективної роботи.
Купив якось неймовірні і дуже складні пазли відомого німецького виробника на чотири тисячі елементів. Приніс своїм учням-програмістам, запропонував скласти. Умови прості – з мене кабінет, робоче місце, вода, бо в кабінеті дуже спекотно. Учні нікому нічого не зобов’язані. Хочеш – приходиш і працюєш, хочеш – ні. Завжди можна сказати «ну не змогла». В куточку до комп’ютера приєднав колонки – самі собі музику під час роботи вибирайте яку хочете. Позичив непогану камеру зі штативом. Отже – беретеся?
На початку очікувано було «вау, зараз ми тут все і відразу». Звичайно почали оптимізувати, бо програмісти. Почали групувати-сортувати елементи. По кольорам, по іншим критеріям. Рамку швидко склали. Нижня частина відрізняється кольором, її також відносно швидко зібрали. А далі стало важко. Море облич, дуже між собою схожих. Почали запрошувати друзів, щоб допомагали збирати. Все одно важко. Можна не прийти, але ж ти розумієш, що там складно і ти б дуже допоміг, якби приєднався. І вони ходили 20 днів і працювали. Лише зранку, бо спекотно і втомлюєся. Більше за все боялися, щоб не загубити хоча б один елемент з чотирьох тисяч, бо ці елементи по всьому кабінету були розкидані. Щодо музики – вони все самі, але дуже здивувася, коли почув Pink Floyd. Запропонував фінальне відео озвучити саме цією піснею. Розказав їм трохи про концептуальність The Wall. Камера знімала всі 20 днів, після чого шкільний інженер-програміст зібрав все у чотири хвилини відео. Всі учасники цього збору вже закінчили школу, дехто і університет, але пазл живе в кабінеті інформатики, дивуючи гостей.
Як на мене, пазли можуть бути чудовою річчю для колективної роботи, достатньо простим і дієвим інструментом формуванням відповідальності в командній роботі, розвитку комунікативних навичок. Да і музики різної цікавої наслухались, там були і тематичні підбірки. Звичайно, настільки складний пазл може не всім колективам варто пропонувати, і не всім такий підкориться. Але концепція, як на мене, цікава, проста і не дуже дорога у реалізації.
На фото – саме цей пазл авторства аргентинського художника Guillermo Mordillo, у відео – 4 хвилини на тему «Як ми це зробили» ))
Частина 2.
Дана стаття як і більшість статей на «Плетиві» - не візія, не концепція, не філософська мета, а опис цілком практичного власного досвіду.
Ціль даної статті: допомогти початківцям купити і зібрати комплект обладнання (контролер + світлодіодна панель), встановити на комп'ютер програмне забезпечення, відкрити проєкт-шаблон, змінити код-приклад, скомпілювати код, залити все, що вийшло в контролер, порадіти )
Особисто я купую обладнання в Китаї, так зазвичай дешевше. Посилка з Китаю, зазвичай, приходить за три-чотири тижня. Якщо не хочеться чекати, все це є в Україні. Можна довго розписувати тонкощі купівель в Китаї та плутати недосвідчених. Тому дам посилання на готові сторінки на aliexpress, знімаючи з себе відповідальність. Я колись там купував, все було добре. Якщо щось прийде несправне або не прийде взагалі – напишіть мені будь ласка на Ця електронна адреса захищена від спам-ботів. Вам необхідно увімкнути JavaScript, щоб побачити її. , позабираю посилання. Я не отримую жодного центу з купівель за цими посиланнями. Вмієте шукати і обирати самі — краще так і зробіть.
Що треба купити?
1. Контролер NodeMCU
Наприклад, тут:
https://www.aliexpress.com/item/32665100123.html
Серед запропонованих пристроїв раджу вибрати таку версію: V3 Nodemcu-CH340
Чіп CH340 служить мостом між мікроконтроллером і USB-портом комп'ютера, що дозволяє завантажити прошивку в плату, а також передавати між собою дані. Ми далі будемо встановлювати драйвер саме для CH340.
Ціна контролера приблизно 70 грн.
2. Світлодіодний модуль MAX7219
Наприклад, тут:
https://www.aliexpress.com/item/32789160918.html
У цього продавця доступні модулі з світлодіодами зеленого і червоного кольору. Мені більше подобається спокійний зелений, а ви можете обрати модуль, який більше подобається вам. Необхідні для підключення проводи йдуть в комплекті.
Ціна приблизно 160 грн.
Все, купувати обладнання більше не треба.
Далі — виконуємо послідовно дану інструкцію і, може, все вийде.
— З’єднуємо контролер і світлодіодну панель згідно схеми проводами з комплекту світлодіодної панелі:
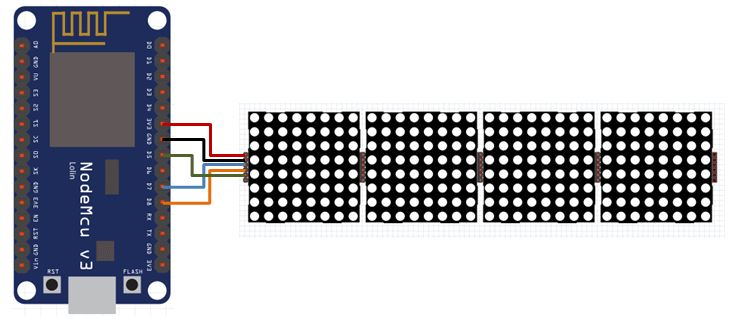
— Скачуємо і встановлюємо драйвер для чіпа CH340G, що забезпечує зв’язок контролера з комп’ютером (для Windows).
— Після встановлення драйверу підключаємо NodeMCU до комп’ютера за допомогою кабеля для зарядки телефона з роз’ємом microUSB. Це дуже популярний кабель, сподіваюсь, знайдеться в господарстві, щоб не купувати.
— Після підключення контролера до комп’ютера треба знайти CH340G в списку пристроїв, що Windows визначила для NodeMCU (в прикладі це COM3):
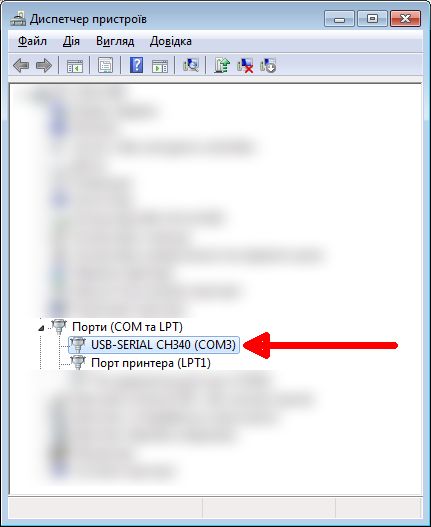
Якщо при підключеному контролері ви бачите, що серед портів з’явився будь-який порт на CH340, то все коректно встановлено. На даному етапі можна відключити контролер від комп’ютера.
— Скачуємо Visual Studio Code з офіційного сайту і встановлюємо.
Для Windows 10 та Windows 11 скачуйте останню версію з сайту. Якщо у вас на комп’ютері встановлено версії Windows нижче 10, вам треба скачати більш стару версії Visual Studio code. Цитата з офіційного сайту: «VS Code will no longer provide product updates or security fixes on old Windows versions. VS Code version 1.70.3 is the last available release for Windows 7 users and version 1.79 will be the last available release for Windows 8 and 8.1 users».
— Запускаємо Visual Studio Code, переходимо в розширення (Extensions), в пошуку починаємо писати PlatformIO IDE, обираємо і встановлюємо розширення (шукайте кнопку Install). Якщо розширення вже встановлено, то ми побачимо, як у мене, Uninstall.
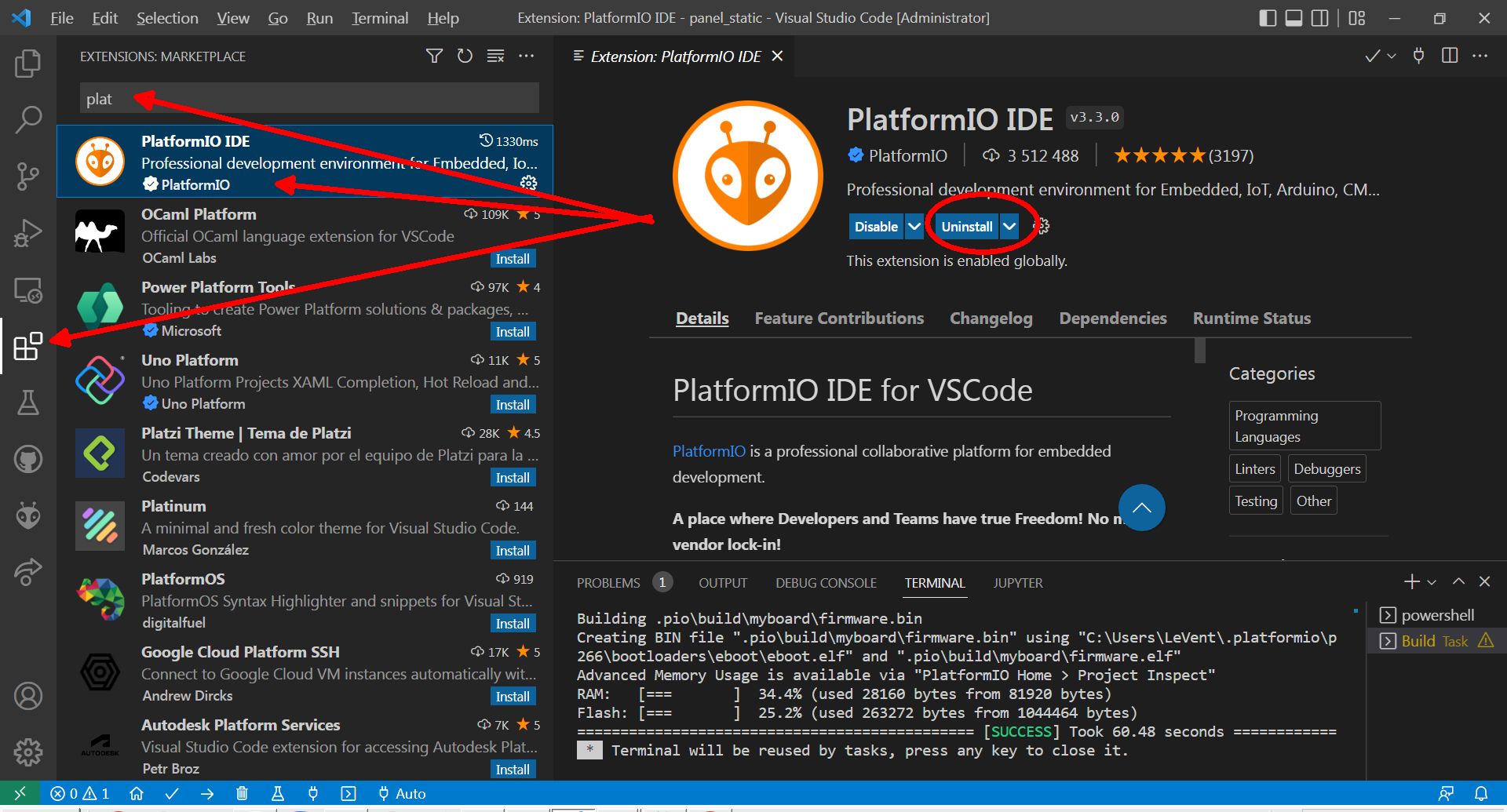
— Скачуємо архів, в якому проєкт-приклад зі всіма необхідними бібліотеками
— Розпаковуємо архів і запам’ятовуємо куди розпакували
— В Visual Studio Code обираємо «File – Open Folder» і обираємо папку, в яку щойно розпакували архів
— Обираємо файл main.cpp з папки src
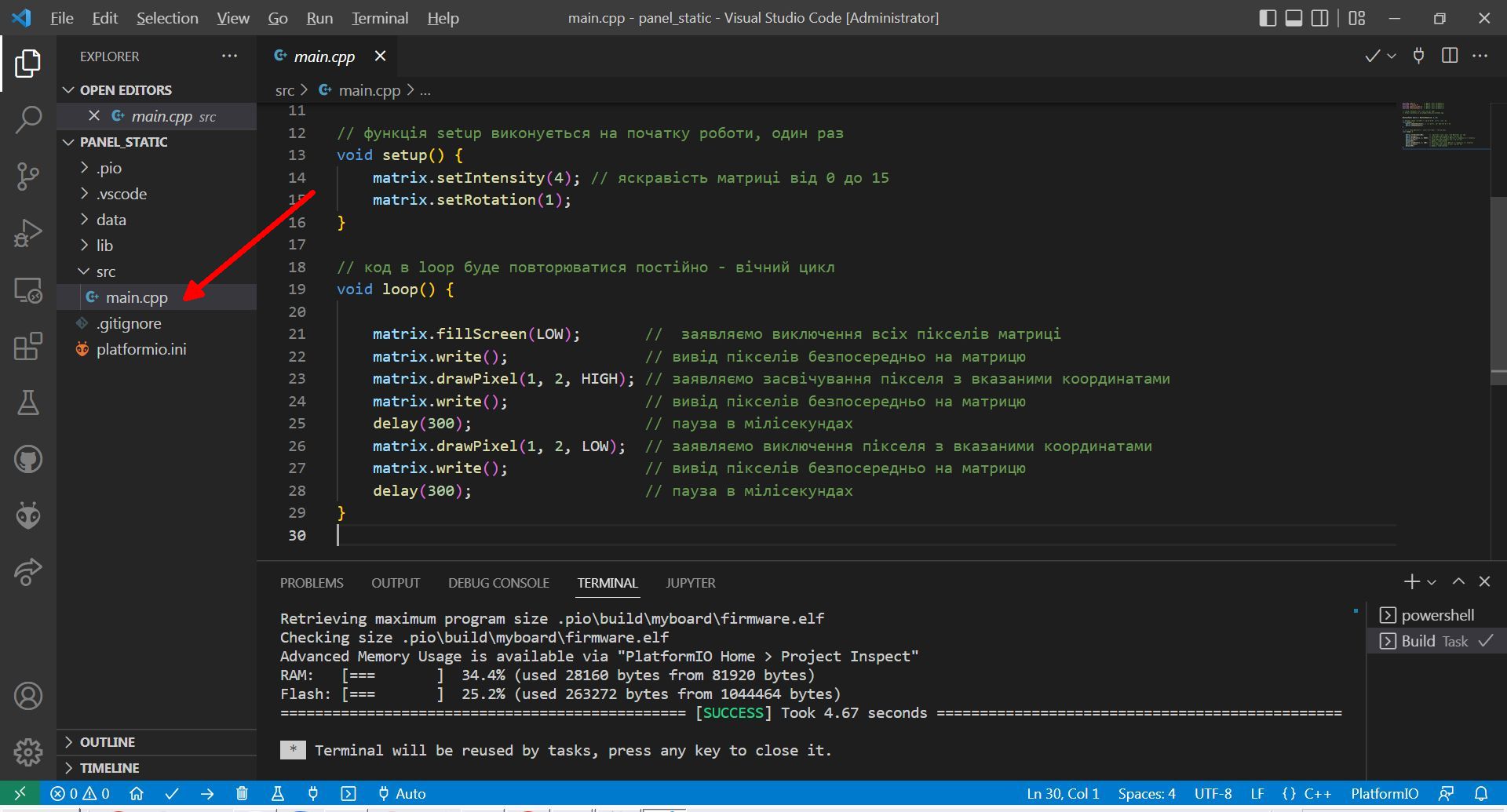
Це і є скетч. Зверніть увагу на 21 рядок і далі.
Хочете засвітити світлодіод?
Визначаєте його координати і засвічуйте. Центр координат — в лівому верхньому куті. Ось як це просто:
matrix.drawPixel(1, 2, HIGH);
(з міркувань продуктивності пікселі відразу не надсилаються на світлодіодну панель. Змінюється лише внутрішній буфер растрового зображення)
matrix.write();
(відправка внутрішнього буферу растрового зображення на світлодіодну панель)
Хочете виключити цей світлодіод?
matrix.drawPixel(1, 2, LOW);
matrix.write();
Використання комбінації «Visual Studio Code + PlatformIO» зручно тим, що весь проект зберігається в одній папці. Тут і основний скетч і всі необхідні бібліотеки відповідних версій. Якщо перенести цю папку на інший комп’ютер, де встановлено «Visual Studio Code + PlatformIO» то все буде так само працювати.
Нашу програму будемо писати у файлі main.cpp
Програмуємо мовою програмування Arduino C. В інтернеті багато прикладів, можна розібратися з синтаксисом. Visual Studio Code підкаже помилки на етапі компіляції скетча.
Залишилось навчитися це все закидувати у контролер. Для цього треба скомпілювати бінарний файл. Натискаємо на «PlatformIO Bild».
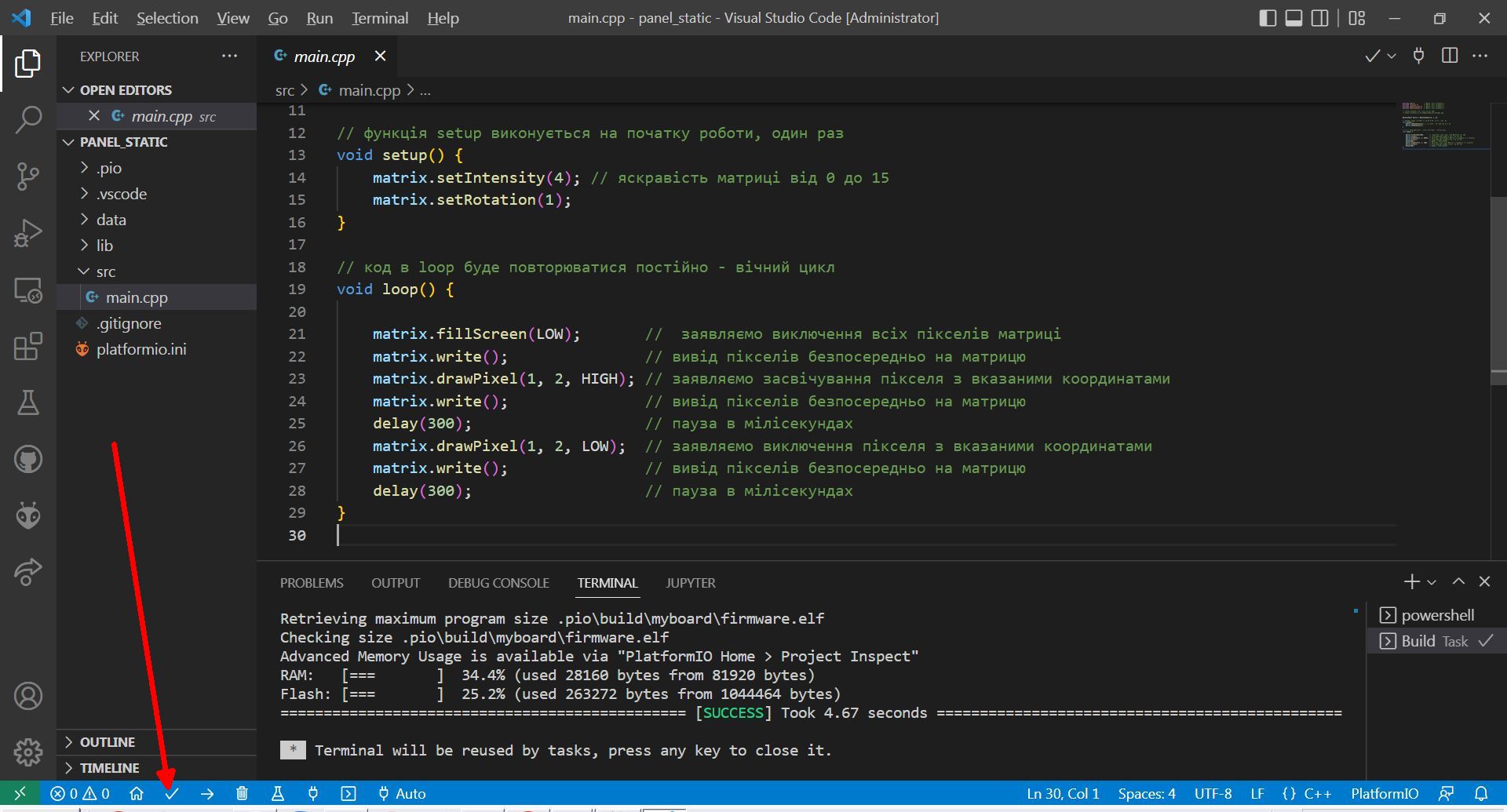
Якщо немає помилок, то в результаті компіляції буде створено бінарний файл. Якщо в скетчі підключаються бібліотеки і в папці проєкту є ці бібліотеки, то все коректно скомпілюється. Дуже зручно. Про успішну компіляцію буде сповіщено чудовим зеленим SUCCESS:
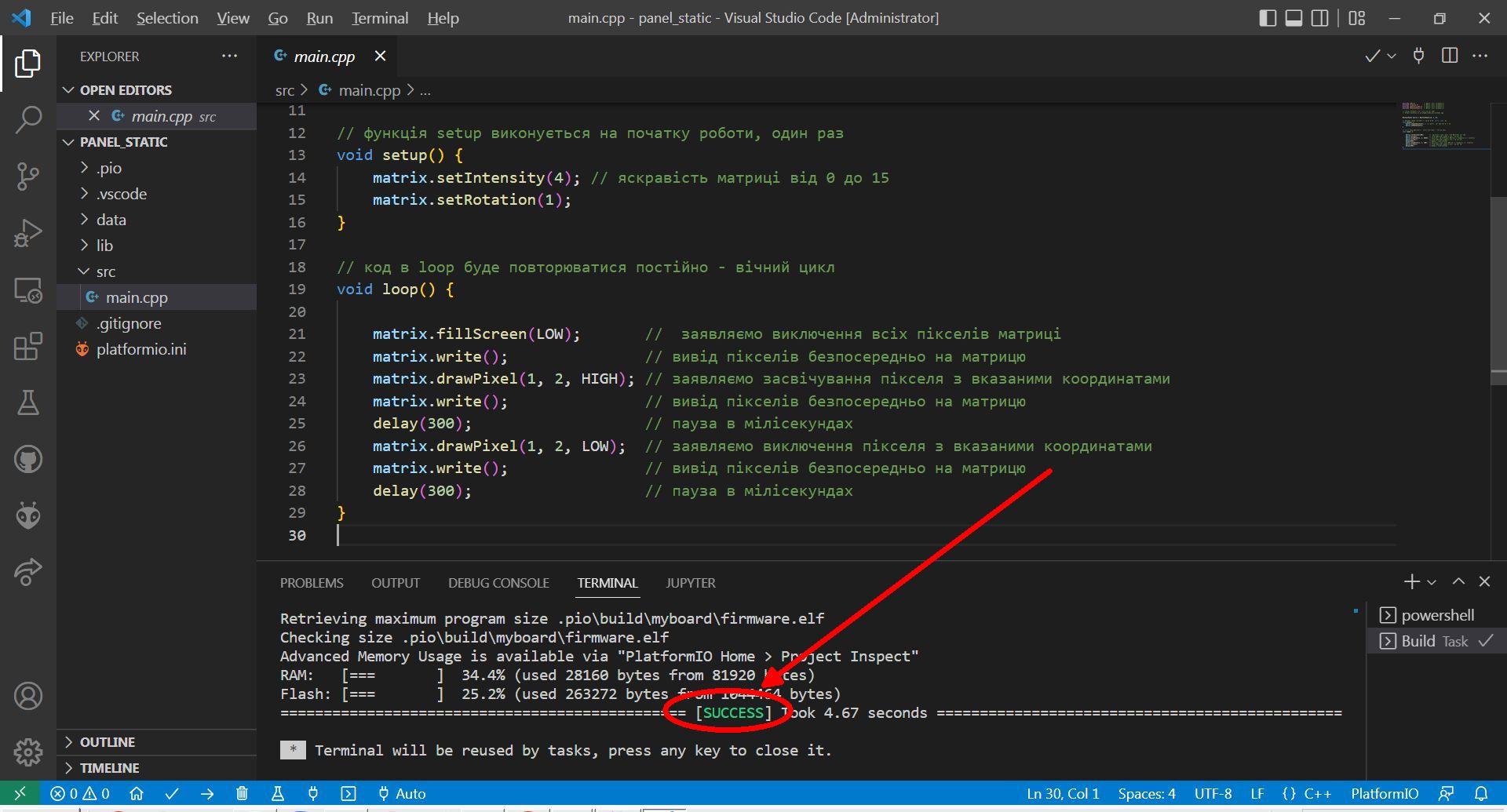
Залишається залити вже скомпільований бінарний файл безпосередньо в контролер.
Для чого необхідно підключити до комп’ютера контролер і натиснути «PlatformIO Upload».
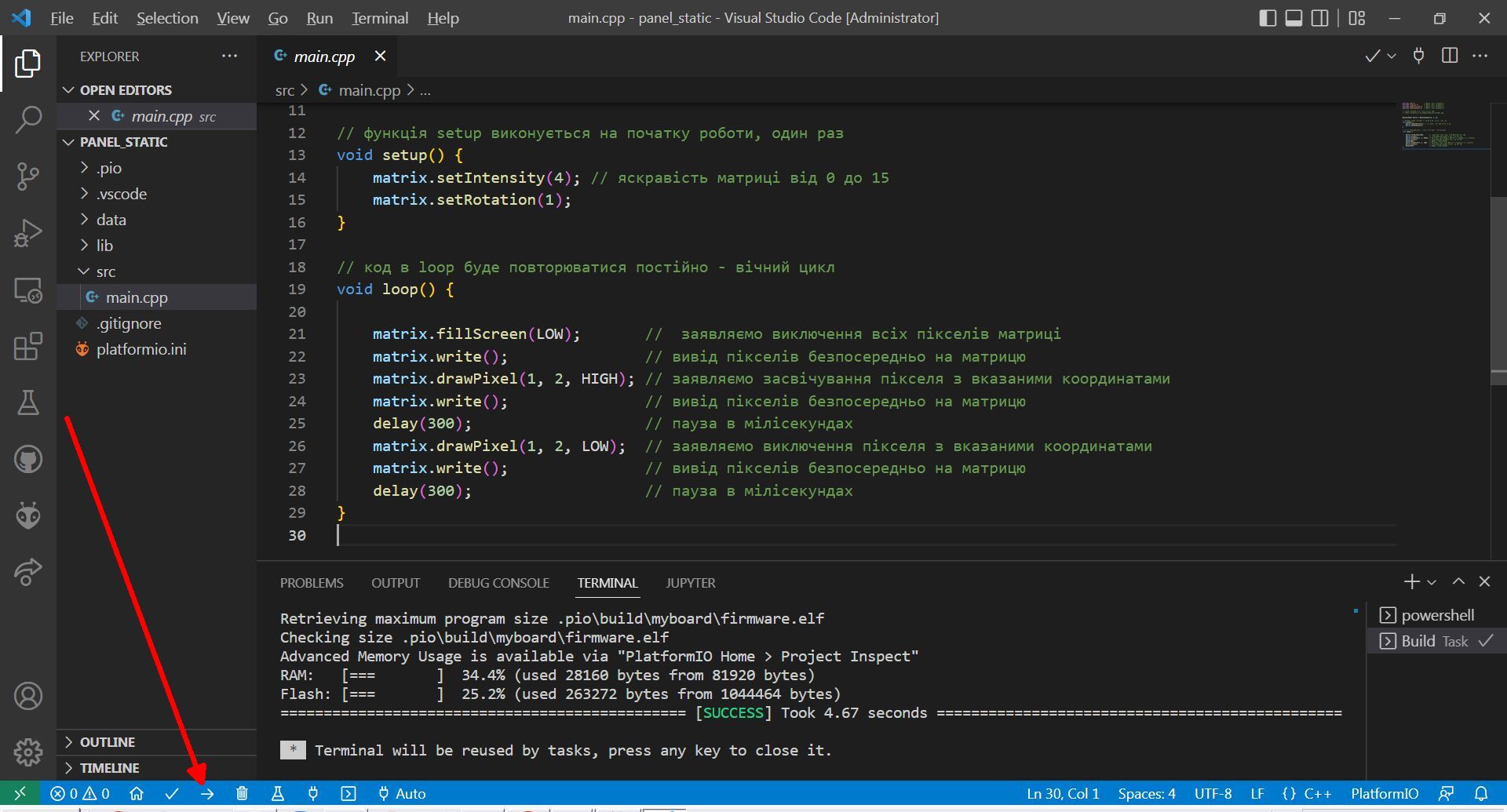
Можна пропустити «PlatformIO Bild» і відразу натискати «PlatformIO Upload», тоді спочатку буде скомпільовано бінарний файл і відразу залито його в контролер.
Це все )
Ось як мигає світлодіод на панелі з прикладу-скетчу.
При роботі в класі, не потрібно багато контролерів і панелей. Учень або група учнів можуть написати скетч і перевірити його на помилки, скомпілювавши бінарний файл. А після того, як звільниться контролер – підключити його до свого комп'ютера, залити в нього бінарний файл і перевірити роботу на реальному пристрої.
З використанням комбінації контролера і світлодіодної панелі можна розбирати цикли (робити усілякі біжучі вогні), крутити тексти (біжучі рядки). Розбирати роботу різних бібліотек. Для тих, хто цікавиться більш глибоко, в контролері NodeMCU є WiFi, тобто можна на контролері підняти вебсервер і керувати контролером по WiFi зі смартфона.
Або нехай контролер щось вимірює і результати роботи кудись відправляє в інтернет, підключившись до шкільного WiFi. Саме так в школі, де я працюю реалізована система моніторингу якості вуличного повітря німецького проєкту «sensor.community». Програмне забезпечення розповсюджується безкоштовно, в самій станції моніторингу, яку ми зібрали, не перший рік працює той самий NodeMCU.
До контролера можна підключати датчики, з контролера можна керувати механізмами управління.
Програмувати можна і на Windows (від версії 7 і далі) і на Лінукс і на MacOS. Visual Studio Code безкоштовна, переважна більшість бібліотек – також.
Кому сподобалось – пробуйте.
Для ознайомлення і старту, сподіваюсь, даної статті і папки-прикладу абсолютно достатньо.
Успіхів!
Анатолій Анатолійович,
липень 2023
Частина 1.
Згідно сучасної концепції української середньої базової освіти, програмування складає вагому частину курсу інформатики. Це імітаційні середовища на кшталт code.org (стаття на Плетиві) , це Scratch, в якому можна створювати цікаві речі. Це багато інших чудових систем і концепцій, що знаходять, пишуть, перекладають і використовують неспокійні душею вчителі. І незважаючи на очевидну революцію штучного інтелекту, в освіті залишаються актуальними ці самі неспокійні вчителі поряд з неспокійними учнями-ачомучками.
Програмування розумних пристроїв. Для чого це може бути корисним? Які проєкти можна реалізувати в даному напрямку?
Реальна задача: систематично вимірЯти вологість ґрунту в вазонах по школі. Не використовувати ж для цього цілий комп’ютер чи ноутбук. Це незручно, дорого. Крім того, треба якось подружити ноутбук і якісь датчик, що безпосередньо буде вставлятися в землю. І потрібно буде носити за собою датчик разом з ноутбуком, дротами і брудними від ґрунту руками.
А якщо купити контролер за 70 гривень, датчик вологості за 100 гривень, невеликий екран за 60 гривень. Все це вкласти в якийсь корпус а для живлення використати звичайний павербанк? Залишиться написати програму для роботи цього пристрою. Завдяки великій кількості бібліотек, програмування такого контролера виходить зовсім нескладним. Особисто у мене програма для такого пристрою вийшла менше 100 рядків коду, більша частина з яких про те, в якому місці екрану і як вивести текст. І більшу частину коду я знайшов в інтернеті, де безкоштовно пояснили деталі. Готовий пристрій був подарований вчительці біології, яка опікується шкільними рослинами.
Ще один приклад з реалізованих – система моніторингу якості повітря в приміщенні, де перебувають люди. Той самий контролер за 70 гривень, екран за 60 гривень, високоточний датчик температури і вологості (DHT22) – 150 гривень, датчик СО2 (MH-Z19B) – тисяча гривень. Останній датчик мені подарували. Програма для даного пристрою у мене вийшла також менше 100 рядків коду. Ось приклад, як воно працює, ще без корпусу:
В реальності екран так не мерехтить. А готовий пристрій моніторить повітря в кабінеті, де я працюю, він виручив нас і при регулюванні системи вентиляції в шкільному укритті.
На цьому самому контролері вже три роки працюють шкільні розумні годинники, що повідомляють про час уроків і перерв, виводять інформаційні повідомлення. Ось опис і відео роботи цього годинника на Плетиві.
Всі ці пристрої я будував на контролері NodeMCU. Він дешевий, в Китаї можна знайти такий за 70 гривен. Це набагато дешевше, ніж, припустимо micro:bit, що розроблений BBC для використання в комп’ютерній освіті Сполученого Королівства, що коштує в Україні біля тисячі гривень. NodeMCU – значно дешевший. Якщо більше немає грошей, то можна лише його купити і вже цього достатньо. Беремо кабель від зарядки телефону (micrоUSB) і підключаємо цей контролер до комп’ютера. На контролері є вбудований світлодіод і ми можемо їм керувати. Запалювати і виключати. Як це робити? Спитайте в інтернеті «NodeMCU blink». Для багатьох першою програмою для контролера і є керування вбудованим світлодіодом.
Якщо є можливість і хочеться трохи більше, то можна докупити ще щось цікаве. Для своїх експериментів я використовую окрім NodeMCU світлодіодну панель MAX7219. Ось так вона виглядає і коштує близько 160 грн.

Щоб з’єднати контролер і панель паяти нічого не треба. Проводи входять в комплект, а для наших експериментів додатковий роз’єм не потрібний.
В січні 2021 року я на своєму гуртку вперше спробував програмування контролерів. На комп’ютери заздалегідь поставив все необхідне програмне забезпечення. В папці-проекті був зразок коду, так званий скетч. Учні відкрили папку, переробили скетч, одним кліком мишки скомпілювали зі скетча бінарний файл та залили його в контролер.

Все відразу і запрацювало, тобто при невеличкій стартовій підготовці програмування контролеру може мати достатньо низький поріг входження.
Ось, результати першого уроку:

Автор – Олександр Соколов

Автор – Дмитро Маловатов
Звертаю увагу – це перший урок. Тобто, немає нічого складного, якщо заздалегідь поставити необхідне програмне забезпечення. Хочете засвітити світлодіод – вкажіть його координати.
Нескладно. Недорого. Цікаво?
В другій частині статті буде покрокова інструкція як зробити таке (тут відео в динаміці):

Пропоную розглянути чудову задачу «Булочки» з сайту eolymp.com. Безумовним плюсом задачі, як на мене, є простота умови і чудова родзинка, яку психологи називають «розрив шаблону».
Булочки
https://www.eolymp.com/uk/problems/11379
Умова:
Хусейн дуже любить булочки, які продаються в університеті. Відомо, що
Хусейн хоче придбати точно n булочок. Яку найменшу кількість гяпиків йому слід витратити?
Вхідні дані:
Три натуральні числа a, b і n, кожне з яких не більше 10^9.
Вихідні дані:
Виведіть найменшу кількість гяпиків, яку слід витратити Хусейну для покупки точно n булочок.
Приклад
Вхідні дані :
2 5 10
Вихідні дані:
17
Автор: Михаил Медведев
Розглянемо тестовий приклад. Одна булочка коштує два гяпіка. Але три булочки коштують не шість, а п’ять гапіків. Ми бачимо зрозумілу оптову ціну. Якщо купити відразу три, то кожна булочка буде трохи дешевше, а саме 5 / 3 = 1,67 гяпіка. Очевидно, що при оптових знижках нам варто купити якомога більше «трійок булочок», а вже далі доповнити нашу купівлю одиночними, більш дорогими булочками.
В тестовому прикладі нам треба купити 10 булочок. Давайте порахуємо максимальну кількість трійок, що ми можемо купити. 10 // 3 = 3. Тобто ми можемо купити три рази по три булочки і таким чином заплатимо 5 + 5 + 5 = 15 гяпіків. Це так ми купимо дев’ять булочок. Ну а десяту вже купимо подорожче, за два гяпіка.
В булочках у нас буде така купівля: три + три + три + одна.
В грошах у нас буде така купівля: 5 + 5 + 5 + 2 = 17.
Ці 17 гяпіків – це і є відповідь, яку ми бачимо в тестовому прикладі.
І якщо ми напишемо код, то здамо задачу… лише на 80%. А чого?
А тому що автор гарно підказав нам типовий приклад. І тому що ми всі звикли, що оптом – дешевше. Це – шаблон. Але… А хто нам обіцяв, що так завжди? А давайте знайдемо розв’язок, коли будуть такі умови:
2 (ціна однієї одиночної булочки)
7 (ціни трьої булочок, от такий дивний опт, а хто сказав, що не буває?)
10 (скільки Хусейну треба купити булочок)
Звичайно, що тоді Хусейну і дарма не треба такі оптові ціни, бо поштучно булочки дешевше.
Гарна задача, так?
То здавайте! )
Відома американська корпорація Autodesk в 2011 році запустила Tinkercad — безкоштовне 3D-моделювання в браузері.
Мета даної статті – короткий огляд можливостей Tinkercad для навчання учнів.
При безкоштовній реєстрації можна вказати, що ви – вчитель і отримати зручні можливості для роботи з учнями. Після реєстрації вчителю можна створити класи, які будуть ізольовані, тобто по замовчуванню проєкти учнів будуть мати статус приватних їх будуть бачити лише самі учні-автори і вчитель. Це дуже зручно для перевірки – вчитель заходить в клас на сайті Tinkercad і переглядає роботи учнів.
Так виглядає меню класів:
Дуже зручно на сайті реалізована система реєстрації учнів. При створенні кожного класу (або групи, якщо клас ділиться на групи) формується окреме посилання, яке передається учням. Особисто я використовую Google Workspace for Education, тому посилання на приєднання викладаю в Google Classroom. Учні групи з Google Classroom переходять за посиланням і можуть зайти в свою групу, використовуючі шкільний корпоративний акаунт:
Ніякої спеціальної реєстрації не потрібно, все просто.
Учні і вчитель можуть станом на 2023 рік створювати три типи проєктів (в системі вони звуться Designs): 3D, Circuits, Codeblocks
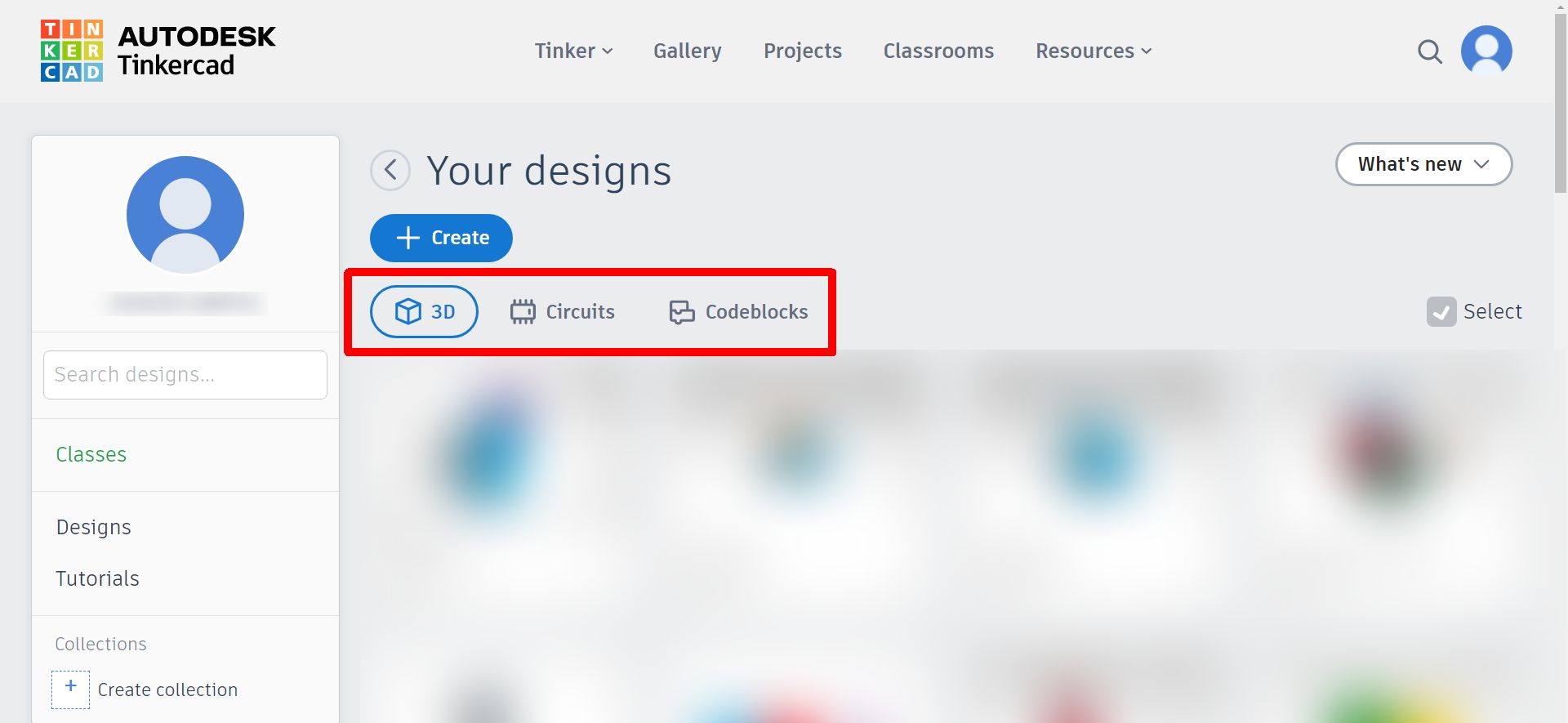
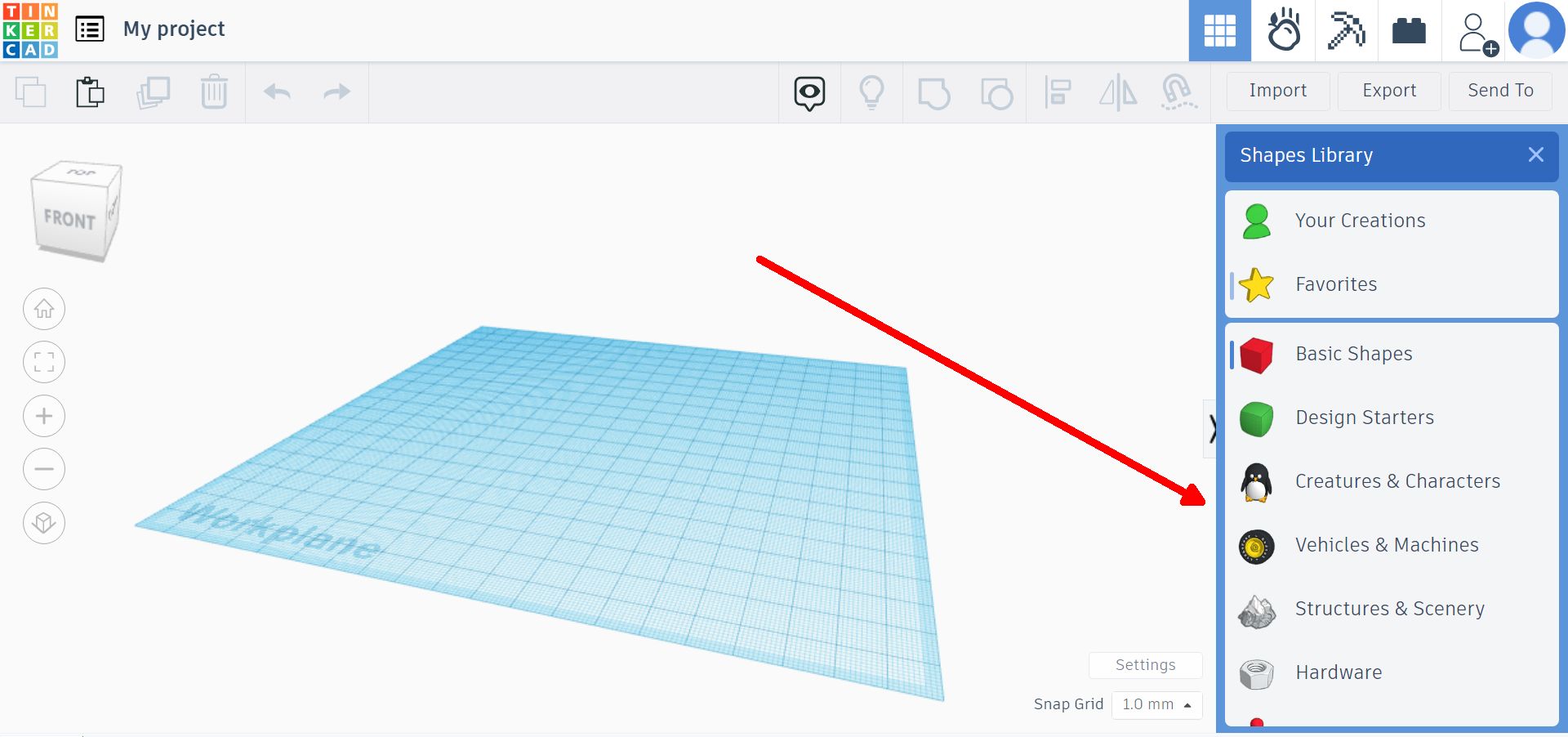
При створенні 3D проєкту можна обирати не лише куби та циліндри, можна малювати в редакторі свої об'єкти а також обирати інші елементи з бібліотеки:
Можна створити проєкт, назвати його і зберегти – для цього натиснути на логотип в лівому верхньому куті. Збережені проєкти можна редагувати.
При роботі доступні інструменти – вирівнювання, групування, зеркалювання. Є Undo, Ctrl+C, Ctrl+V також працюють.
Це – поганий приклад, примітивний, але свій )
Достатньо цікавим є створення проєктів в Circuits. Ми з учнями згадували фізику, паралельне і послідовне з’єднання. Міряли тестером струм, що тече через світлодіод, а потім проводили симуляцію цього в Circuits. Підбирали струмообмежуючий резистор для світлодіоду при використанні дев’ятивольтової батареї (тим, кому більше 40 років знають її з іменем «Крона»).
Ось приклад симуляції, обмеження струму світлодіоду підбором резистора:
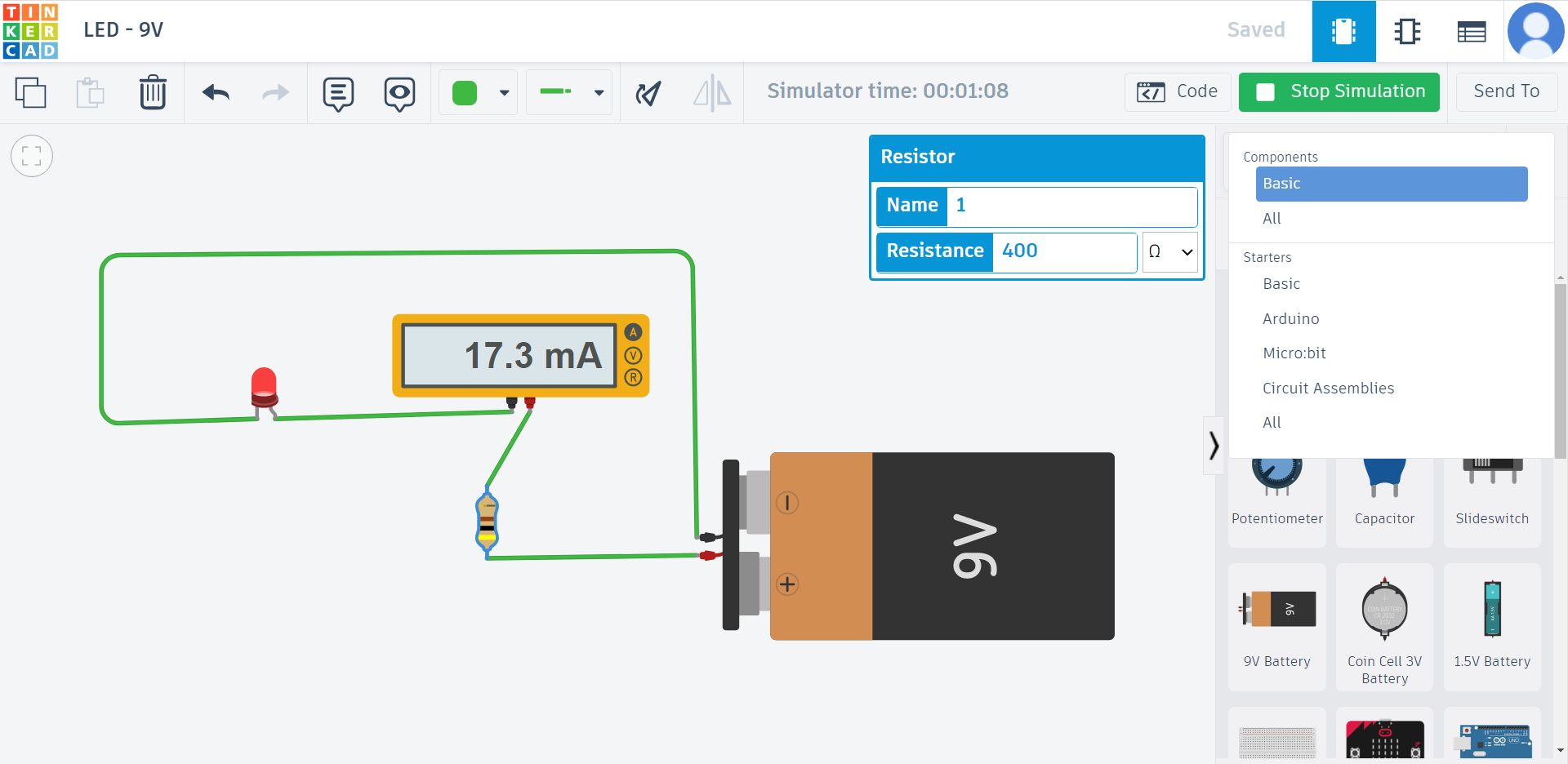
Варто звернути увагу, в системі є можливість симуляції з використанням Arduino та Micro:bit
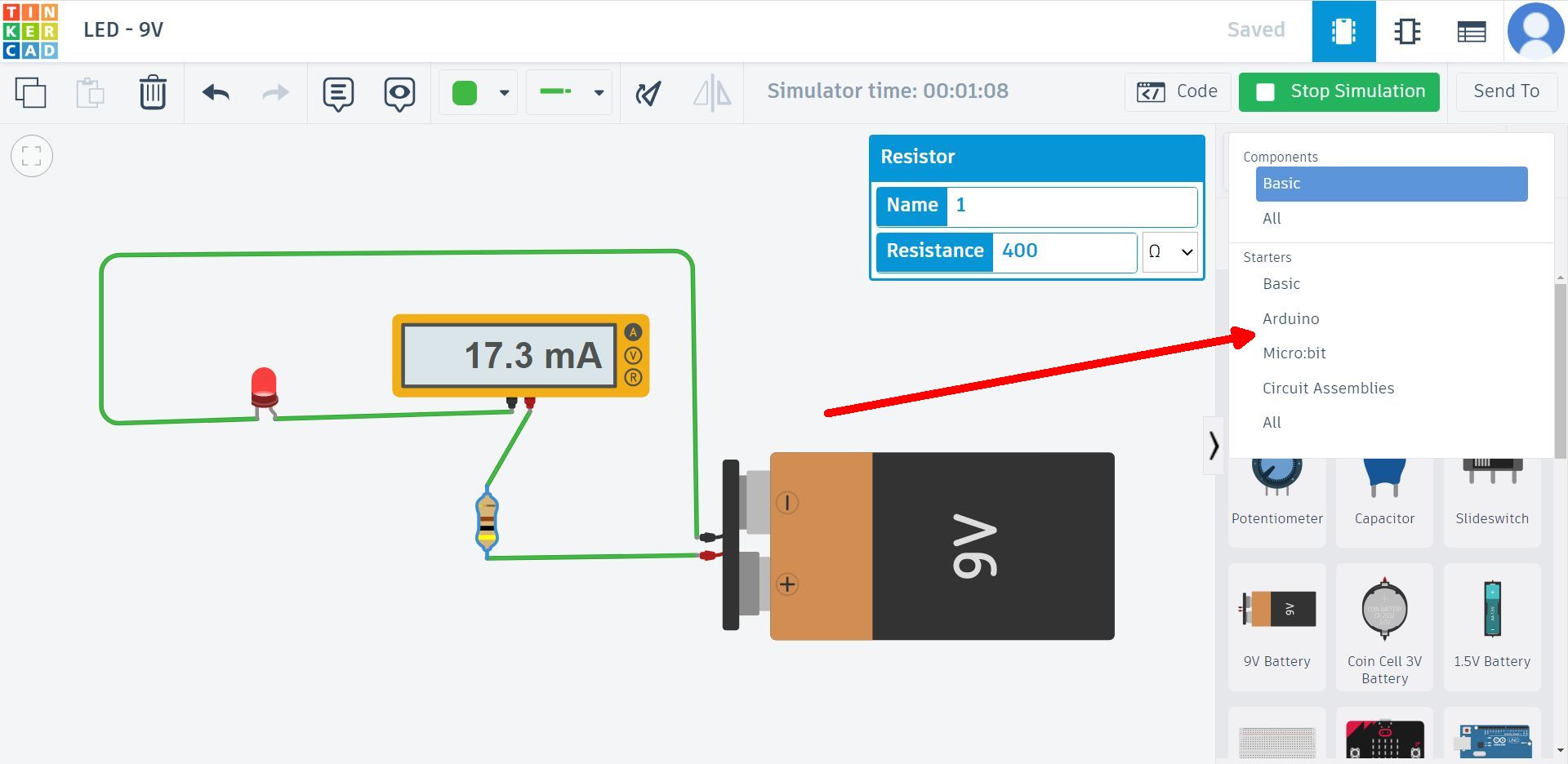
І третій тип проєктів – Codeblocks, який буде зрозумілим всім любителям блокового програмування. В даному типі проєктів можна з блоків складати програми. Ось приклад, танцюючий Мурчик )
Складаємо програму, запускаємо на виконання – працює.
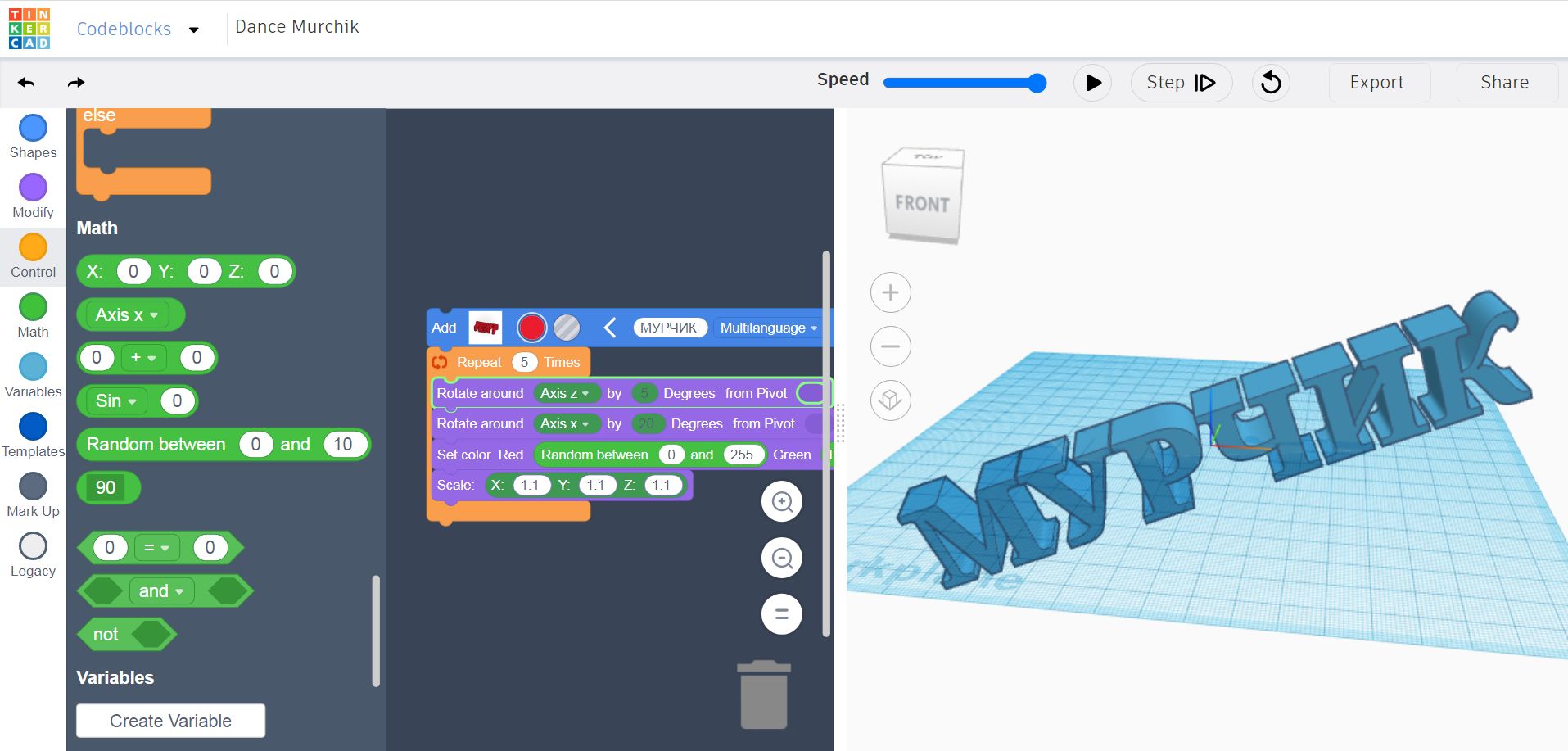
Безумовно, Tinkercad – це не 3ds Max – топовий продукт корпорації Autodesk. З іншої сторони, чи багато шкіл можуть купити 3ds Max? Ось прайс з офіційного сайту:
А ще варто проаналізувати ефективність 3sd Max в звичайній школі. Безумовно, ніхто не зменшує чудові можливості безкоштовного Blender.
При цьому простий, зрозумілий, з низьким порогом входження Tinkercad, як на мене, вартий уваги.
Анатолій Анатолійович,
червень 2023
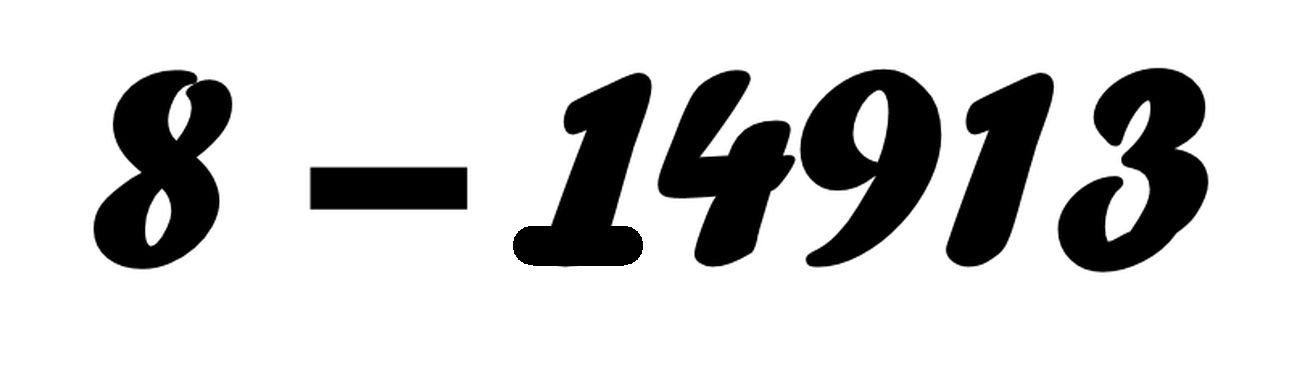
Особисто мені дуже подобаються задачі з кількома розв’язками. Вони навчають споглядати світ навколо з різних сторін.
Одну з таких задач і пропоную вашій увазі.
Я побачив одне рішення, моя учениця Анастасія – ще одне. А, можливо, їх ще більше – аргументованих рішень?
Спробуйте спочатку самостійно знайти кілька рішень, а лише потім переглянути вже знайдені, натиснувши "Детальніше"